2-1. Оценка математического ожидания и дисперсии
Пусть имеется случайная величина X с математическим ожиданием mx и дисперсией Dx и п результатов независимых опытов Х1, Х2, ..., Хn. Необходимо определить состоятельные оценки для mx и Dx [Л. 21]. Возьмем
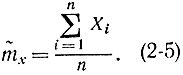
Оценка 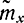 - состоятельная, так как по закону больших чисел она по вероятности сходится к mx. Она и несмещенная, так как
- состоятельная, так как по закону больших чисел она по вероятности сходится к mx. Она и несмещенная, так как
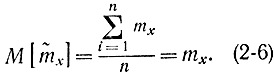
Дисперсия величины 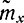
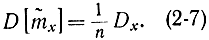
Можно показать, что если величина X распределена по нормальному закону, то дисперсия (2-7) будет минимальной и, следовательно, эффективной в смысле критерия минимума дисперсии.
Перейдем к оценке дисперсии. Оказывается, что оценка
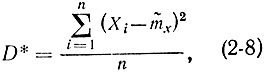
где
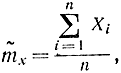
является смещенной. Действительно,
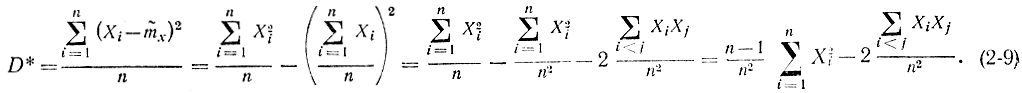
Возьмем математическое ожидание от этой оценки
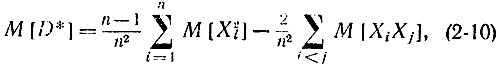
выберем начало координат в точке mx. Очевидно, что от этого дисперсия не изменится. Тогда
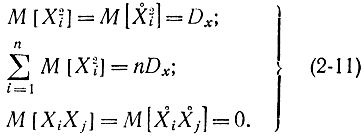
Последнее неравенство (2-11) справедливо в силу независимости опытов. Подставив (2-11) в (2-10), получим:
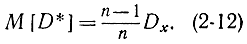
Отсюда видно, что величина D* не является несмещенной оценкой, так как ее математическое ожидание не равно Dx. Чтобы оценка стала несмещенной, ее следует умножить на n/(n-1), в результате получим:
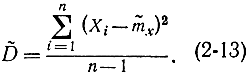
Отличие оценки 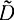 от D* существенно только при малых n (меньших 10). При больших n они близки, так как n-1≈n.
от D* существенно только при малых n (меньших 10). При больших n они близки, так как n-1≈n.
Проверим состоятельность обеих оценок. По определению а называется состоятельной оценкой параметра ã, если для любого
ε>0:
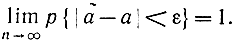
Используя неравенство Чебышева, легко получить достаточное условие состоятельности оценки
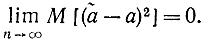
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'