2-2. Приближенные методы определения доверительных интервалов для оценок математического ожидания и дисперсии
Вначале рассмотрим случай определения доверительного интервала при заданной дисперсии [Л. 21]. Согласно формуле (2-5) оценка 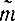 =
=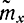 математического ожидания равна арифметической сумме независимых одинаково распределенных случайных величин Xi Согласно центральной предельной теореме она распределена по закону, близкому к нормальному при достаточном числе слагаемых. Математическое ожидание
математического ожидания равна арифметической сумме независимых одинаково распределенных случайных величин Xi Согласно центральной предельной теореме она распределена по закону, близкому к нормальному при достаточном числе слагаемых. Математическое ожидание 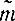 равно m:
равно m:
М [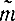 ]=m.
]=m.
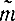 ]=m.
]=m.Дисперсия оценки математического ожидания
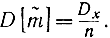
Найдем такую величину ε, чтобы удовлетворялось равенство
Р {[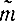 -m]&360;ε}=β. (2-14)
-m]&360;ε}=β. (2-14)
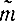 -m]&360;ε}=β. (2-14)
-m]&360;ε}=β. (2-14)С помощью Ф*(х) эту вероятность можно определять приближенно, пользуясь формулой
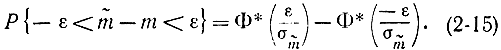
Очевидно, что
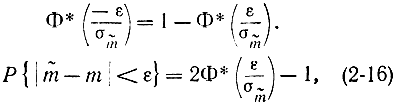
где
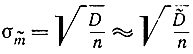
- среднеквадратичное отклонение оценки m. Приняв
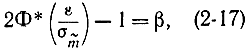
найдем:
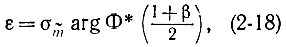
где argФ*(z) обозначает функцию, обратную Ф*(z).
С помощью этих величин определяем доверительный интервал:
Jβ(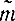 -σ
-σ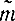 tβ,
tβ, 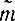 +σ
+σ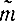 tβ) (2-19)
tβ) (2-19)
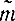 -σ
-σ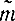 tβ,
tβ, 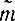 +σ
+σ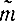 tβ) (2-19)
tβ) (2-19)Пример 2-1. При подсчете времени проезда на автобусе от одной конечной остановки до другой была составлена табл. 2-1.

Таблица 2-1
Найдем оценку среднего времени проезда (математического ожидания времени проезда), дисперсии и определим доверительный интервал для оценки математического ожидания при доверительной вероятности β=0,95.
- В качестве оценки
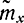 примем
примем
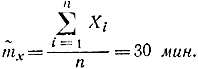
- В качестве оценки Dx возьмем:
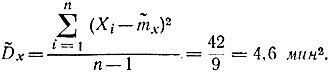
- Дисперсия оценки математического ожидания
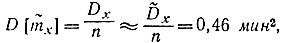
- Доверительный интервал для оценки математического ожидания при доверительной вероятности β=0,95 определим по формуле
Используя таблицы функций Ф*(х) (приложение 1), найдем:
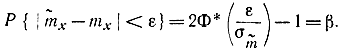 т. е. доверительный интервал для
т. е. доверительный интервал для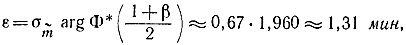
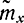 Jβ={30 - 1,31; 30+1,31}=(28,69; 31,31), мин.
Jβ={30 - 1,31; 30+1,31}=(28,69; 31,31), мин.
Аналогично определяют доверительные интервалы для дисперсии и получают ее несмещенную оценку
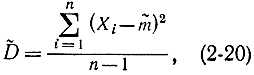
где
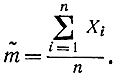
Согласно формуле (2-13) оценка дисперсии является суммой случайных величин (Xi - т)2/(п- 1), которые, однако, не являются независимыми, так как m зависит от всех X. Но можно показать, что при увеличении n закон распределения этой суммы приближается к нормальному. Определим математическое ожидание и дисперсию оценки дисперсии. Как было показано,
M[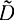 ]=D.
]=D.
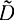 ]=D.
]=D.Аналогично можно получить формулу для дисперсии оценки дисперсии:
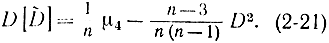
Если бы было возможно подсчитать по этим формулам математическое ожидание и дисперсию оценки дисперсии 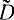 , то, используя формулу, аналогичную (2-19), можно было бы определить доверительный интервал для дисперсии. Однако для определения дисперсии по формуле (2-21) необходимо знать D и μ4. Вместо D можно подставить его оценку
, то, используя формулу, аналогичную (2-19), можно было бы определить доверительный интервал для дисперсии. Однако для определения дисперсии по формуле (2-21) необходимо знать D и μ4. Вместо D можно подставить его оценку 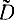 , а вместо μ4 - величину, равную
, а вместо μ4 - величину, равную
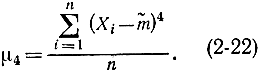
Но эта оценка дает невысокую точность даже при достаточно большом числе опытов. Поэтому получим формулы для частных случаев, когда закон распределения величины X нормальный или равномерный. В первом случае можно выразить четвертый момент через дисперсию:
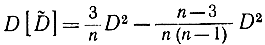
Подстановка этого выражения в формулу (2-21) дает:
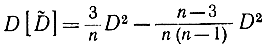
или
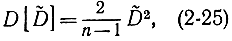
Заменив D2 его оценкой, получим:
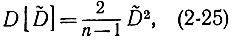
откуда,
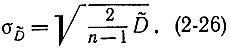
Для равномерного закона распределения в интервале [α,β] имеем:
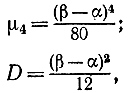
откуда
μ4=1,8D2. (2-27)
Подстановка этого выражения в формулу (2-21) дает:
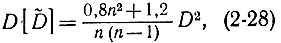
откуда приближенно получаем:
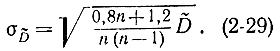
Если закон распределения неизвестен, то целесообразно все же использовать формулы, справедливые для нормального закона, при условии, что закон распределения не обладает явной асимметрией.
После того как ориентировочно определено значение дисперсии оценки, находим доверительный интервал
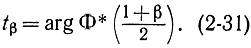
Величина tβ определяется по заданной доверительной вероятности β с;помощью таблиц нормального закона (см. приложение 1) по формуле
tβ= argΦ*(1+β/2). (2-31)
Рассмотрим пример на определение доверительного интервала для оценки дисперсии.
Пример 2-2. Чтобы решить вопрос о качестве нового ружья, проводится пристрелка его в тире, причем качество оценивается по величине дисперсии случайной величины X - расстояния от центра мишени до точки попадания. Распределение величины X близко к нормальному. Пусть по 20 выстрелам определили оценку ее дисперсии 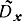 =0,64 см2. Определим доверительный интервал для оценки дисперсии Dx при доверительной вероятности Р = 0,8:
=0,64 см2. Определим доверительный интервал для оценки дисперсии Dx при доверительной вероятности Р = 0,8:
- По формуле (2-26) определяем:
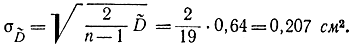
- С помощью таблиц Φ*(x) находим:
В результате J=(0,64-0,27; 0,64 + 0,27)=(0,37; 0,91).
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'