2-3. Точные методы построения доверительных интервалов

Все рассмотренные выше методы были приближенными. Дело в том, что закон распределения оценки зависит от закона распределения величины X и, следовательно, его параметров, которые неизвестны. Поэтому и доверительный интервал J_β зависит от этих неизвестных параметров. Замена этих параметров их оценками 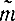, 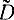никак не обоснована, и при этом неясно, какая получается погрешность. Можно полагать, что она будет небольшой. Однако применение таких оценок не требует (по крайней мере для оценки математического ожидания) знания закона распределения случайной величины.

Точные методы построения доверительных интервалов не требуют такой замены оценками, так как они исходят из того, что параметры закона распределения величины X неизвестны.

Ниже будут рассмотрены точные методы оценки для случайной величины X, подчиненной нормальному закону распределения. Основная идея точных методов состоит в том, что от исходной случайной величины X переходят к некоторой другой величине Т (или V), распределение которой не зависит от параметров величины X, а только от числа измерений n и вида закона распределения величины X.

Начнем с оценки дисперсии [Л. 21, 24, 26]. Воспользуемся теоремой, известной из теории вероятностей: сумма квадратов независимых случайных величин, распределенных по нормальному закону с нулевым математическим ожиданием и единичной дисперсией, распределена по закону χ² с n степенями свободы. Введем случайную величину

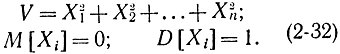
Плотность распределения случайной величины по закону χ² с n степенями свободы определяется формулой

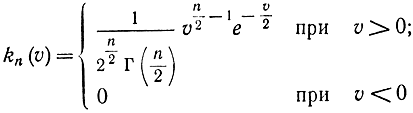
или

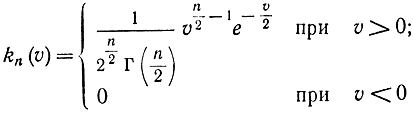
где

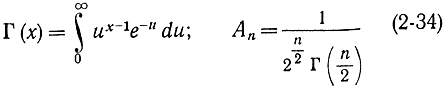
- известная гамма-функция, для которой составлены таблицы. Рассмотренную теорему можно обобщить на случай величины

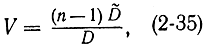
в которой значение 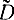соответствует оценке (2-20). Эта величина имеет распределение χ² с n-1 степенями свободы. Но она не удовлетворяет условиям теоремы в части независимости слагаемых. Дело в том, что

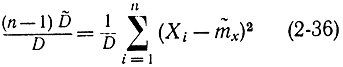
представляет собой сумму квадратов n зависимых случайных величин Y_i=X_i-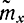, которые удовлетворяют одному условию

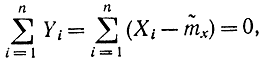
так как для 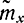имеем определение (2-5).

В соответствии с этой формулой можно выразить одно Y_i через все остальные. Поэтому в правой части формулы (2-36) стоит сумма квадратов (n-1) независимых случайных величин, распределенных по нормальному закону с нулевым математическим ожиданием и единичной дисперсией.

Отсюда следует, что случайная величина X распределена по закону χ² с n-1 степенями свободы, т. е.

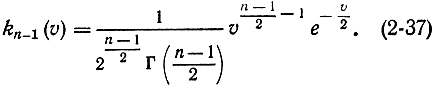
На этом примере очень четко иллюстрируется понятие числа степеней свободы. Группа законов распределения, таких как χ²-распределение, распределение Стьюдента и пр., связана с понятием n независимых случайных величин. Если они зависимы, то к ним не применима выше рассмотренная теорема и они на первый взгляд не подчиняются этим законам распределения. Но если можно точно выявить связь (как в выше рассмотренном примере), то всегда за счет уменьшения числа величин можно добиться их независимости. Для этого при наличии l связей следует выразить любые l случайных величин через остальные n-l. Тогда исходная величина может быть представлена не как сумма n зависимых, а как сумма n-l независимых случайных величин, к которой можно применять теоремы, справедливые только для сумм независимых случайных величин.

Из теории вероятностей известно, что математическое ожидание и дисперсия случайной величины, которая распределена по закону χ² с n-1 степенями свободы, имеют вид:

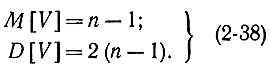
Из этих выражений и формулы (2-33) очевидно, что параметры и закон распределения случайной величины, имеющей распределение χ², не зависят от параметров исходной случайной величины.

Чтобы получить доверительные интервалы для дисперсии, необходимо выразить оценку 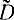через величину V. С помощью соотношения (2-35) имеем:

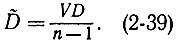
Зная закон распределения V, можно всегда найти интервал J_β, в который попадает эта величина с вероятностью β. Трудности в построении этого интервала состоят в том, что χ²-распределение несимметрично (рис. 2-1). Поэтому условимся выбирать доверительный интервал для V при равенстве вероятностей выхода этой величины влево и вправо за этот интервал (это означает равенство заштрихованных на рис. 2-1 площадей):

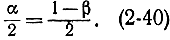
Заметим, что вероятность непопадания в интервал J_β равна V. Обычно в таблицах (приложение 2) приводятся значения функции переменной χ² для r степеней свободы, т. е. значения вероятности

Для r=n-1 по таблицам находят χ₁², соответствующие p₁=α/2, и χ₂², соответствующее p₂=1-α/2. Тогда для величины V

Нетрудно убедится, что доверительный интервал для дисперсий исходной величины определяется с помощью формулы (2-42), так как неравенства

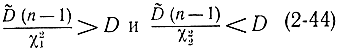
равносильны неравенствам

потому что

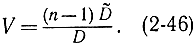
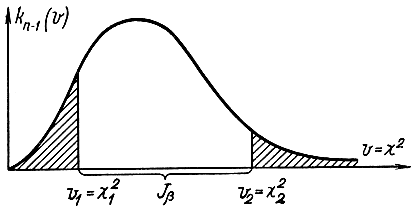
Рис. 2-1. Вид кривой распределения вероятности по закону χ²

Пример 2-3. Применительно к условию примера 2-1 определим доверительный интервал для оценки дисперсии 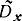при β=0,8 и n=20. Имеем: (n-1)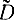=12,8см²; α=1-β=0,2. Из таблиц χ²-распределения при r=19 (см. приложение 2) находим χ²₁=11,65, которое соответствует p=1-α/2=0,9, и значение χ²₂=27,2, которое соответствует p=α/2=0,1. Отсюда согласно формуле (2-43) имеем:

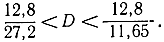
Тогда искомый доверительный интервал для оценки дисперсии

Теперь рассмотрим аналогичный точный метод определения доверительного интервала для математического ожидания. Если бы была известна дисперсия Dx - cr* величины X, то этот доверительный интервал приблизительно можно было бы определить с помощью таблиц нормального распределения, использовав нормированную величину

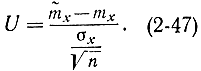
Действительно, входящая сюда величина (2-5) как сумма n независимых случайных величин имеет закон распределения, который стремится с ростом n к нормальному закону (в соответствии с центральной предельной теоремой) с дисперсией и математическим ожиданием

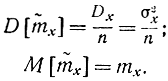
Оказывается, что если в выражении (2-47) σ_x заменить на 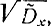, то величина

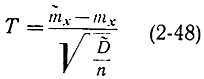
будет иметь распределение Стьюдента с n-1 степенями свободы, зависящее только от номера n, и поэтому не надо знать величину дисперсии. Действительно, можно сформулировать и доказать следующую теорему: если величина Т равна отношению двух случайных величин

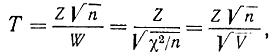
где Z - нормально распределенная величина с нулевым, математическим ожиданием и единичной дисперсией, a W - независимая от Z величина и V=W² распределена по закону χ² с n степенями свободы, то при этих условиях случайная величина Т подчиняется закону распределения Стьюдента с n степенями свободы (или t-распределению), которое задается формулой

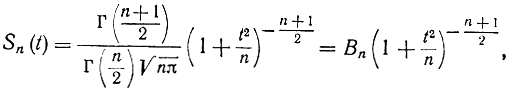
где

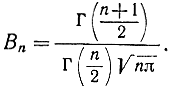
Для доказательства найдем сначала плотность совместного распределения величин Z и V. Поскольку по предположению Z и V независимы, то их совместная функция плотности есть произведение функции плотности z и v:

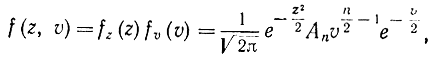
где

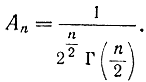
Затем получим:

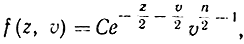
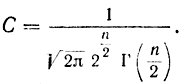
функция распределения величины Т

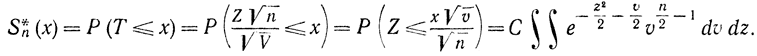
Область интегрирования определяется неравенствами 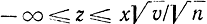и представляет множество точек плоскости (z, v), ограниченное ветвью параболы 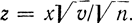Выполняя двойное интегрирование сначала по z от - ∞ до 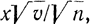, затем по v от 0 до ∞, находим:

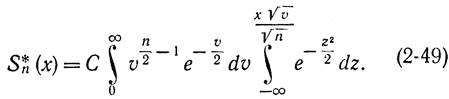
Для определения плотности распределения величины Т продифференцируем равенство (2-49) по х в правой части под знаком интеграла

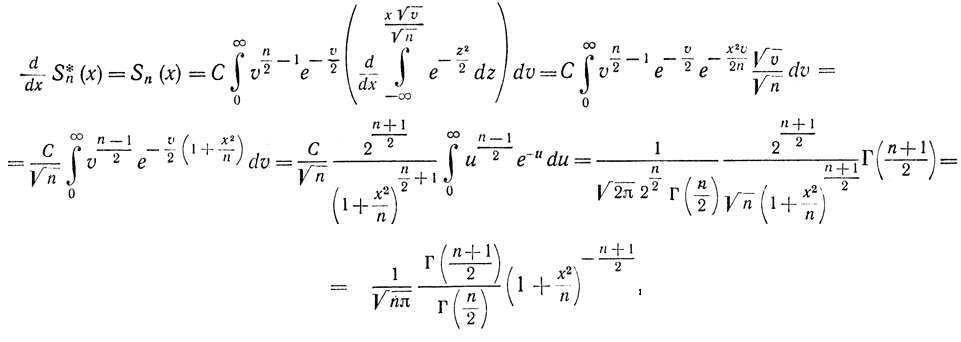
при этом выполнена замена переменных

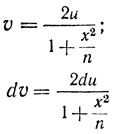
и подставлено выражение для С. Теорема доказана.

Чтобы применить эту теорему к величине (2-48), проверим выполнимость ее условий. Ранее было показано, что среднеарифметическое 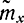нормальной выборки х распределено нормально с математическим ожиданием М[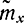]=m_x и дисперсией 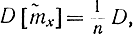т. е. величина

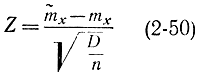
имеет нормальное распределение с параметрами (0, 1). Далее показано, что оценку (2-13) можно выразить через величину V, распределенную по закону χ² с n-1 степенями свободы, следующим образом:

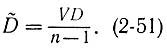
Отсюда с учетом (2-50) и (2-51) формула (2-48) будет иметь вид:

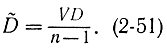
т. е. величина Т подчиняется распределению Стьюдента с n-1 степенями свободы:

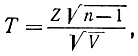
Эта функция - симметричная и при n→∞ стремится к нормальному закону с нулевым математическим ожиданием и единичной дисперсией. Кроме того, в силу симметрии имеем:

В данном случае доверительный интервал можно взять симметричным относительно значения 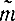. Обозначим половину этого интервала через ер и найдем его из соотношения

Р 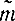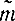{|- m |<ε_β}=p. (2-54)

Перейдем от величины 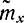к величине T, распределенной по закону Стьюдента. Для этого умножим обе части неравенства |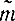-m|<ε_β на 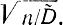. Тогда формула (2-54) перепишется в виде

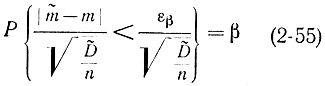
или

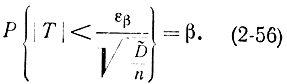
Введя величину

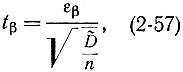
получим:

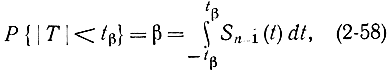
так как функция S_n-1(t) является функцией распределения для Т. В силу четности S_n-1(t) можно написать:

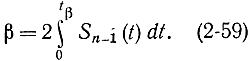
Если составлены таблицы функции (приложение 3)

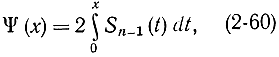
то, взяв обратную функцию от Ψ(х)

можно определить доверительный интервал t_β. Однако для удобства сразу составляют таблицу обратных функций (2-61). По найденному из нее значению t_β находят:

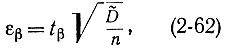
и

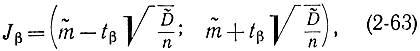
Пример 2-4. Определим математическое ожидание и дисперсию (среднеквадратичное значение) ошибки системы автоматического управления. Уравнения движения объекта и системы управления наберем на вычислительной машине, а процесс управления смоделируем в реальном масштабе времени. Значение ошибки будет фиксироваться на фотографической пленке и в определенный момент считываться. Для набора статистики повторяем моделирование и запись. Необходимо выяснить, сколько потребуется решений задачи, чтобы доверительный интервал для оценки математического ожидания ошибки при β=0,9 составлял определенную величину. Для оценки этой величины определим доверительный интервал для различного числа опытов. В результате моделирования получим табл. 2-2 значений ошибки.

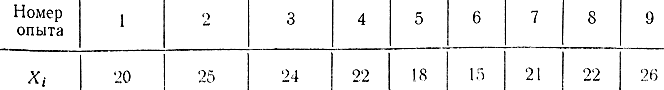
Таблица 2-2

Для n=9, n-1=8 и β=0,9 из таблиц распределения Стьюдента (приложение 3) находим t_β=1,86. Пользуясь полученной табл. 2-2, с помощью формул (2-5) и (2-13) получаем:

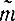= 21,6 м; 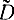= 11,8 м

откуда

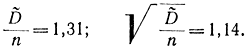
В результате девяти опытов имеем:

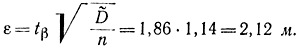
Следовательно, для получения интервала ±1 м девяти опытов мало. Нетрудно убедиться, что 2,12/21,6≈10%. Поэтому можно считать, что точность определения математического ожидания при девяти опытах составляет 10%.

Пример 2-5. Вы с товарищем отправляетесь путешествовать. Сколько денег необходимо взять с собой? Так как вы путешествуете впервые, то советуетесь с компетентными людьми и составляете табл. 2-3.

Таблица 2-3

Сколько же вам взять денег?

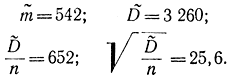
Вы считаете для себя допустимой доверительную вероятность β₁=0,9. Ваш товарищ не любит рисковать и считает, что событие достоверно при β₂=0,99. Вычисляем доверительные интервалы для этих значений:

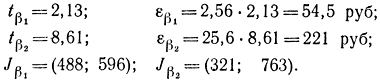
Следовательно, вы будете настаивать взять 596 руб. с гарантией 0,9, а ваш товарищ - 763 руб. с гарантией 0,99.

Сколько же вам взять денег? Тут вы начинаете припоминать, что в 5 случаях из 8 ваш друг ошибался, т. е. р₂=3/8=0,4; 1-р₂=0,6; а вы ошибались в трех случаях из восьми, т. е. р₁=0,6; 1-р₁=0,4. Поэтому нужно взять 665 руб. в соответствии с формулой:

Важная особенность точных методов определения доверительных, интервалов в том, что они справедливы для любого малого числа опытов. Однако они требуют, чтобы закон распределения величин в опытах был нормальным. Приближенные же методы справедливы при большом числе опытов, когда сумма их результатов распределена по нормальному закону. Большое число опытов в случае применения приближенных методов необходимо еще и для того, чтобы формулы для подсчета величин 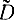и 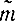давали точный результат.

У точных методов есть большое преимущество перед приближенными методами, так как они не требуют знания дисперсии и математического ожидания.