2-4. Определение доверительных интервалов для вероятности
В настоящее время, когда вероятностные методы прочно вошли в инженерную практику, важно уметь определять доверительные интервалы для оценки вероятности по частотам р*. Например, эффективность систем управления ракетами или эффективность стрельбы неуправляемыми снарядами практически определяется путем многократного повторения выстрелов. Требуется определить, сколько пусков снарядов следует сделать для того, чтобы с вероятностью β отличие частоты р* от вероятности поражения цели р не превышало малой величины εβ , т. е.
Р{|р*-р |&360;εβ}=β.
В последнее время с развитием кибернетики и вычислительных машин для определения вероятности широко используется метод статистического моделирования (метод Монте-Карло) на ЦВМ. Для этого весь процесс управления с учетом случайных воздействий также моделируется на цифровой вычислительной машине. В этом случае необходимо определить число решений для получения требуемого доверительного интервала.
Частоту появления событий р* можно рассматривать как среднеарифметическое
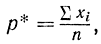
где Xi - число появлений события в i-м опыте. Случайная величина xi может принимать значения 1 с вероятностью р и 0 - с вероятностью q=1-р.
Оценка р* является несмещенной, так как
М[р*] = р.
Дисперсия оценки
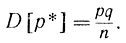
Можно показать, что эта дисперсия является минимально возможной, т. е. оценка р* является эффективной [Л. 21, 26].
Построение доверительных интервалов для величины р* полностью аналогично их построению для математического ожидания, однако так как дисперсия и математическое ожидание в данном случае связаны между собой, то задача существенно упрощается. Предположим вначале, что число опытов достаточно велико и величина р* подчиняется нормальному закону распределения (опыты как всегда считаются независимыми). Будем считать, что величина р не слишком мала и велика. Практически установлено, что достаточно, чтобы nр и nq были больше четырех. Тогда доверительный интервал определяется в соответствии с формулой
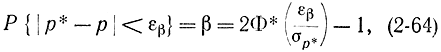
где
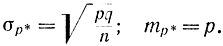
С помощью таблиц (приложение 1) находим:
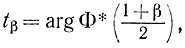
и отсюда
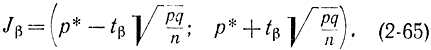
Однако здесь неизвестны р и q. В приближенных расчетах можно было
просто заменить:
pq=p*(1-p*)
и
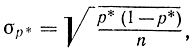
где p* определяется из опыта. Однако в данном случае представляется возможным построить более точную процедуру вычислений. Действительно, согласно формуле (2-65) с вероятностью β выполняется неравенство
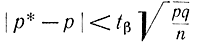
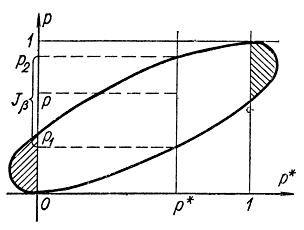
Рис. 2-2. Пояснение к формуле (2-69)
или, возведя обе части неравенства в квадрат, получаем:
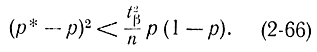
Геометрически это неравенство определяет внутренность эллипса (рис. 2-2) на плоскости p, р* проходящего через точки (0, 0) и (1,1). Чем больше n, тем уже эллипс. Очевидно, что Jβ можно определять следующим образом: по найденному экспериментально р* провести прямую, параллельную оси ординат, и определить две точки пересечения с эллипсом. Значения р, соответствующие этим точкам пересечения, дают доверительный интервал
Jβ=(p1,p2)
Значения р1 и p2 могут быть определены аналитически, если решить уравнение эллипса
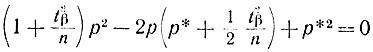
относительно р. В результате
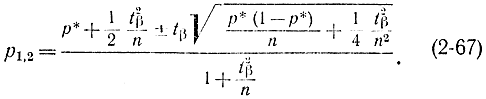
При больших n формула примет вид:
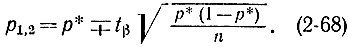
Формулой (2-68) можно пользоваться при больших n (порядка сотни), если р не очень малое и не очень большое, такое, что nq и pq порядка 10 и более.
Пример 2-6. Установим точность определения вероятности поражения самолета ракетой по результатам моделирования поражения на ЦВМ, если произведено 100 моделирований по методу Монте-Карло и получена частота р*=0,7.
Зададимся доверительной вероятностью P*=0,99 и определим по формуле (2-67) доверительный интервал. Считаем, что удовлетворяется условие предельной теоремы и р* подчиняется нормальному закону. По таблицам находим tβ=2,58 и
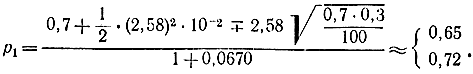
Отсюда
Jβ=(0,65; 0,72).
В соответствии с формулой (2-71) приближенно
Jβ=(0,663; 0,737).
Таким образом, точность монте-карловского моделирования с вероятностью р= 0,99
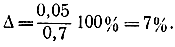
Приближенный расчет дает результаты, отличные от точного на
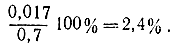
Из приведенного примера видно, что доверительный интервал несимметрично располагается относительно р* при точном расчете, что нетрудно увидеть и на рис. 2-2. Приближенный метод, формула (2-68) и формула Лапласа - Муавра дает симметричное расположение.
Случай малого числа опытов. Если число измерений мало, то величина р* не подчиняется нормальному закону и следует пользоваться непосредственно биномиальным распределением Бернулли. Известно, что вероятность появления в n опытах события m раз определяется формулой
pm,n=Cmnpmqn-m,
где р - вероятность появления события при каждом опыте (опыты считаются независимыми). Это биномиальное распределение Бернулли в отличие от нормального несимметрично, поэтому нельзя взять доверительный интервал симметричным относительно математического ожидания. Кроме того, частота в биномиальном законе - величина прерывистая и поэтому вероятности попадания в интервал, равной β, может и не существовать. Поэтому следует поставить задачу следующим образом: по наблюденной частоте p*=k0/n определить доверительный интервал Jβ=(p1, p2)
такой, чтобы
P{|p*0-p|<εβ}=β. (2-69)
где
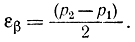
В этом случае доверительный интервал
Jβ=(p*0-ε, p*0+ε),
а условие (2-69) перепишется в виде
P{p1<p<p2}=β. (2-70)
Границы интервала - случайные величины, так как они зависят от случайной величины р*.
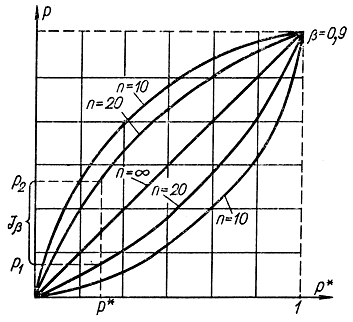
Рис. 2-3. Графика зависимости p и p* при различных n
Можно показать, что верхняя граница p1 определяется из равенства
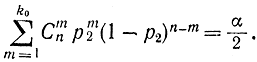
Аналогично нижняя граница р1 доверительного интервала определяется из равенства
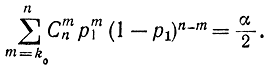
Таким образом, практически доверительные границы определяются по заданной доверительной вероятности β и наблюденной частоте p*0=k0/n, причем должны быть известны в отдельности k0 и n.
Чтобы не решать приведенные выше уравнения, пользуются таблицами (приложение 4) и номограммами (рис. 2-3), которые строят следующим образом: по оси абсцисс откладывают наблюденную частоту p*=p*0=k0/n, по оси ординат - вероятность. Для разных n наносят кривые (для каждой n - две). Пересечения соответствующей ординаты с двумя кривыми дают два значения для концов доверительного интервала. Для каждой доверительной вероятности (3 строят свое семейство кривых.
Пример 2-7. Произведено шесть выстрелов по движущейся мишени. В четырех случаях цель поражена. Каков доверительный интервал для оценки величиной?
p*=4/6=0,67 вероятности поражения при доверительных вероятностях β=0,95 и β=0,99?
По таблицам приложения 4 находим доверительные интервалы:
Jβ=(0,223; 0,957) при β=0,95;
Jβ=(0,144; 0,981) при β=0,99.
Это означает, что погрешности составляют в первом случае 55%, во втором случае 62%. Если семь раз из десяти цель поражена, то
Jβ=(0,348; 0,933) при β=0,95;
Jβ=(0,265; 0,963) при β=0,99.
Если из ста выстрелов попали в цель восемьдесят, то
Jβ=(0,755; 0,895), β=0,95;
Jβ=(0,679; 0,891) β=0,99.
Здесь уже точность составляет 10%.
Определение доверительных интервалов по результатам малого числа опытов позволит спланировать опыты на будущее. Таким образом, в рассмотренной задаче содержатся элементы такого важного и интересного раздела кибернетики, как планирование эксперимента.
На практике встречаются задачи определения доверительных интервалов, когда вероятность события или очень мала, или очень велика. В этом случае находят только одну верхнюю или нижнюю границу доверительного интервала, так как другая равна нулю или единице. Для конкретности рассмотрим вариант с малым р. Точный метод построения доверительного интервала на основе биномиального распределения в данном случае применим, но можно поступить проще. Допустим, что в результате n опытов событие А не появилось ни разу. Назовем это состояние событием В. Требуется найти максимальное значение вероятности наступления события A, т. е. р=р2, для которого вероятность непоявления события при n опытах (вероятность события В) будет меньше α=1-β. Очевидно, что вероятность ненаступления события А при независимых опытах равна:
р{B}=(1-р)n (2-71)
Полагая р(В)=α, получаем:
(1-р)n=1-β, (2-72)
откуда
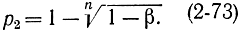
В случае малой вероятности р легко получить формулу для числа опытов n, при которых обеспечивается заданная верхняя граница Доверительного интервала р2 при заданной доверительной вероятности β. Для этого прологарифмируем обе части уравнения (2-73). В результате после несложных выкладок получим искомую формулу в виде
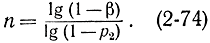
Можно еще больше упростить приведенные выше формулы. Известно, что при малом р биномиальное распределение можно заменить приближенно распределением Пуассона с параметром λ=np [Л. 21], т. е. вероятность появления m раз события, вероятность р которого мала, при n испытаниях следует подсчитывать не как
pm,n=Cmnpn(1-p)m
а как
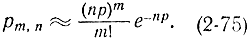
Полагая в формуле (2-78) m=О, получаем
p0,n≈e-np
Действительно, при малом р формулу (2-71) можно приближенно записать в виде
р(В)≈1-np≈e-np.
Тогда вместо формул (2-73) и (2-74) получим:
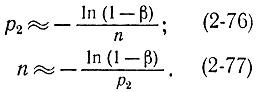
Пример 2-8. Производство телевизоров на заводе представляет собой случайный процесс. Однако вероятность р невыполнения плана мала. При статистических исследованиях оказалось, что в 100 наблюденных случаях план ни разу не был сорван. Определим верхнюю границу р2 95%-ного доверительного интервала для вероятности р. С помощью формулы (2-73), учитывая, что β=0,95, получаем:
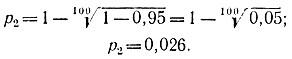
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'