а) Оценки первого и второго моментов
Выбор интервала наблюдения. Известно, что для оценки математического ожидания и корреляционной функции стационарного процесса R(τ) используются следующие выражения [Л. 27-30]:
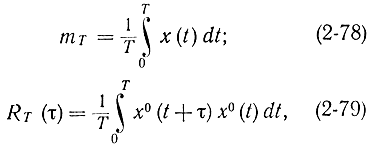
где х°(t)=х(t)-mx.
Определим необходимое значение интервала наблюдения Т, чтобы среднеквадратичная погрешность, обусловленная конечностью Т, не превосходила заданной величины. Обе эти оценки - несмещенные, так как
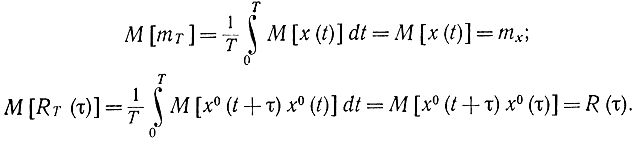
В этих формулах знак математического ожидания М можно понимать как усреднение по времени, так и по ансамблю; более строже и корректнее считать, что этот знак означает усреднение по ансамблю.
Для определения точности оценок найдем их дисперсию
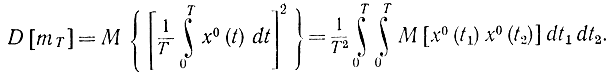
Положив θ=t2-t1 получим:
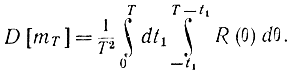
Интеграл такого типа будет встречаться часто, поэтому рассмотрим его особо. Изменим порядок интегрирования, для чего обратимся к рис. 2-4. С помощью рисунка нетрудно убедиться в справедливости соотношений:
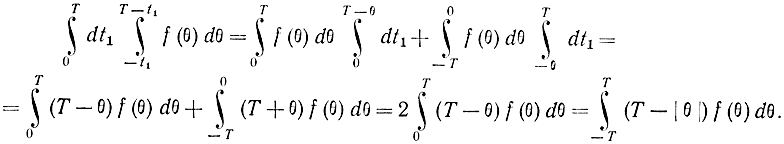
Здесь использовано свойство четности функции f(θ). Применяя эти формулы, получаем:
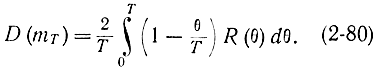
Аналогично дисперсия оценки корреляционной функции
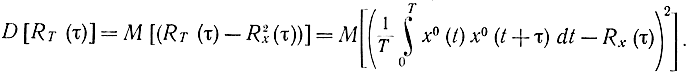
Введем в рассмотрение случайный процесс z(t)=x0(t) х0(t+τ) с математическим ожиданием mz=Rx(τ), не зависящим от t. Предполагая, что z(t) стационарен, по крайней мере в широком смысле [Л. 23], аналогичным образом получаем:
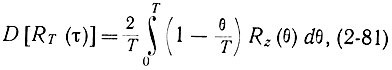
где
Rz(θ)=M{[z(t)-Rx(τ)]*{z(t+θ)-Rx(τ)]}=M{[x0(t)x0(t+τ)-Rx(τ)]*[x0(t+θ)x0(t+θ+τ)-Rx(τ)]}
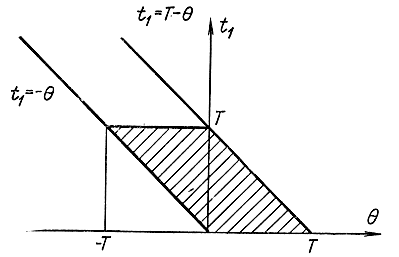
Рис. 2-4. Пояснение к выводу формулы (2-83)
Отсюда видно, что в общем случае дисперсия оценки корреляционной функции выражается через корреляционную функцию процесса х(t) и его смешанный центральный момент четвертого порядка, так как
Rz(θ)=М[х0(t)х0(t+τ)x0(t+θ)х0(t+τ+θ)]-R2x(τ).
При этом следует учесть, что функция Rx(τ) - детерминированная и ее можно выносить за знак математического ожидания; кроме того,
М[х0(t)x0(t+τ)]=М[x0(t+θ)x0(t+θ+τ)]=Rx(τ).
Очевидно, использование формулы (2-81) в общем случае затруднено, так как четвертый момент процесса х(t) неизвестен. Поэтому поступают следующим образом. Предполагают, что четыре величины x1 х2, х3, х4 имеют нормальное совместное распределение, тогда для четвертого момента справедливо соотношение [Л. 27]:
М[x1х2х3х4]=m12m34+m13m24+m14m23, (2-82)
где mij=М[xixj].
Положим:
x1=x(t1); x2=x(t2);
x3=х(t1+τ); х4=х(t2+τ),
тогда
m12=M[х (t1) х(t2)]=R(θ);
m13=M[х (t1) х(t1+τ)]=R(τ);
m14=M[х (t1) х(t2+τ)]=R(θ+τ);
m23=M[х (t2) х(t1+τ)]=R(τ-θ);
m24=M[х (t2) х(t2+τ)]=R(τ);
m34=M[х (t1+τ) х(t2+τ)]=R(θ);
С помощью этих соотношений формула (2-82) может быть записана в виде
М [х(t1) х(t2) х(t1+τ) х(t2+τ)]=R2(θ)+R2(τ)+R (θ+τ)R(τ-θ).
Подставляя эту формулу в выражение (2-81), получаем:
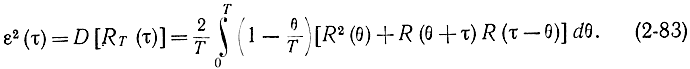
Для определения точности оценки по этой формуле необходимо знать корреляционную функцию процесса. В подавляющем большинстве случаев она имеет вид:
R(τ)=Се-α|τ| cosβτ.
Для такой функции корреляции с точностью до членов порядка малости 1/Т2 имеем:
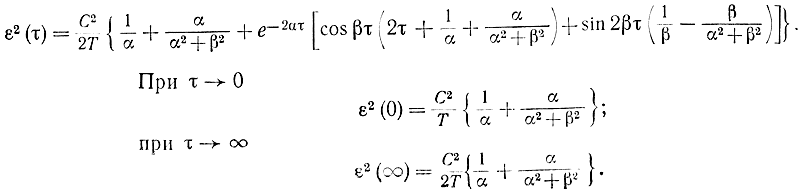
Для того чтобы ошибка в вычислении корреляционной функции (методическая ошибка) не превышала 5% R(0) при τ=0, т. е.
ε2(0)≤0,05R(0),
следует выбирать интервал наблюдения исходя из условия
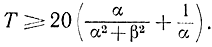
Так, при α=0,2 1/сек и β=π/2 1/секТ ≥102 сек.
Выбор вычислительных параметров. Дадим практические рекомендации по выбору параметров при вычислении функции корреляции [Л. 28-30]. Как уже отмечалось, корреляционная функция оценивается интегралом
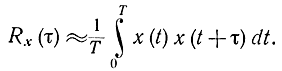
При вычислениях этот интеграл заменяют суммой. Для этого интервал наблюдения разбивают на N интервалов
T=NΔ.
Тогда
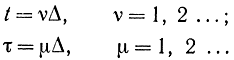
и интеграл можно заменить суммой
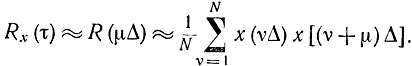
Или, полагая
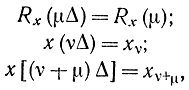
получаем:
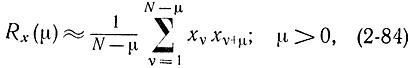
так как при
v≥N-μ xv+μ=0
Аналогично вычисляется взаимная корреляционная функция
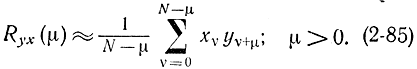
Чтобы определить необходимые для расчета параметры Δ, N и др., рассуждают следующим образом. Любой стационарный случайный процесс можно представить как сумму синусоидальных сигналов со случайными фазами и амплитудами, причем последние не коррелированы между собой:
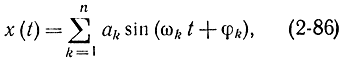
где φk - случайная фаза; ωk - детерминированная частота, а
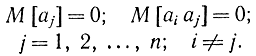
Величина Ak=М[а2k] представляет значение спектральной плотности при частоте ωk Рассмотрим какую-нибудь одну гармонику
х(t)=asin (ωt+φ), (2-87)
где a, ω, φ могут принимать любые значения аk, ω*, φ* (k=1,2,...,n). Для простоты считаем, что а, φ, ω - постоянные величины. Тогда корреляционная функция процесса (2-87)
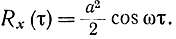
При конечном интервале наблюдения Т выражение для корреляционной функции имеет вид:
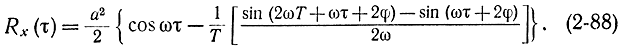
Второй член в этом выражении определяет ошибку, возникшую вследствие конечности интервала наблюдения. Эта ошибка имеет порядок 1/ωΤ и убывает с ростом Τ. Но ωΤ=2πΤ/Τ0, где Τ0 - период, соответствующий частоте ω. Так как в формулах (-2-84) и (2-88) для данного μ используется интервал Т=(N-μ)Δ, а не ΝΔ, то
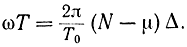
Поэтому для обеспечения 2%-ной точности расчета следует взять:
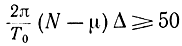
или
NΔ-μΔ≥8T0. (2-89)
Из вышеизложенного следует, что точность вычисления корреляционной функции зависит от интервала наблюдения Т и максимального τ или μ, соответствующего этому τ. При условии 2%-ной ошибки значение τмакс можно выбирать исходя из
|R(τ)|≤0,02|R(0)| (2-90)
при τ≥τмакс. Однако для использования этой формулы необходимо знать саму корреляционную функцию. Поэтому величину τмакс выбирают исходя из максимального периода, который имеется в процессе, или из требования самой низкой частоты fмин, которую необходимо "уловить" в корреляционной функции и спектральной плотности. Например, пусть полоса АСР составляет 1 гц. Для определения флюктуационных ошибок системы рассчитывают спектральную плотность помех на входе. Очевидно, что в этом случае достаточно взять fмин=0,01 гц, так как при частотах f<0,05 гц амплитудно-частотная характеристика системы и спектральная плотность помехи на входе сохраняют постоянные значения.
При известной величине fмин определяется τмакс
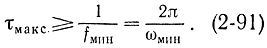
Формулу можно пояснить следующим образом. Как известно, корреляционная функция гармонической составляющей частоты со равна:
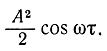
Очевидно, для того чтобы составляющая частоты ωмин выявилась в корреляционной функции, необходимо, чтобы τ приняла все значения от 0 до τмакс, определяемой формулой (2-91). При этом на кривой корреляционной функции получится полный период (рис. 2-5).
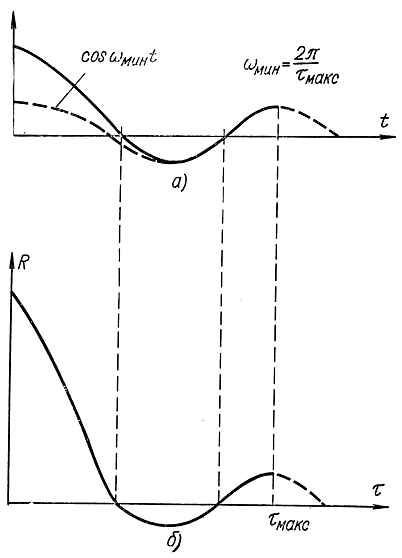
Рис. 2-5. Пояснения к определению τмакс при расчете корреляционной функции а - график исходного процесса с периодической составляющей cosωмин; б - график соответствующей корреляционной функции.
Перейдем к рассмотрению методики определения величины Т. Согласно формуле (2-88) при конечном Т на ошибку главным образом оказывают влияние низкие частоты, так как величина ω стоит в знаменателе, поэтому в первом приближении Т можно определить по ωмин. При 2%- ной точности из формулы (2-88) имеем:
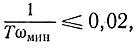
откуда
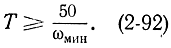
Сравнивая неравенства (2-91) и (2-92), получаем следующую зависимость:
T≈10τмакс (2-93)
При выборе шага Δ поступают следующим образом. Путем многочисленных вычислений корреляционной функции для гармонического сигнала устанавливают, что ошибка будет меньше 2% при шаге
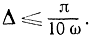
Подставляя наивысшую частоту процесса ωмакс, получают следующую расчетную формулу:
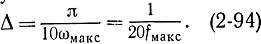
Поясним смысл этого соотношения. Во-первых, значение Δ должно быть настолько мало, чтобы случайный процесс менялся незначительно за время Δ. Кроме того, перед расчетом обычно стараются выделить максимальную частоту случайного процесса, до которой спектральную плотность случайного процесса следует вычислять точно. Так, если случайный процесс воздействует на следящую систему, полоса которой ограничена частотой fмакс (рис. 2-6), то очевидно, что спектральную плотность следует рассчитывать до частоты fмакс, так как более высокие частоты случайного процесса никакого влияния на работу системы не оказывают. Для воспроизведения синусоидального сигнала по заданным дискретным значениям достаточно знать его значения в пяти или десяти точках [в формуле (2-94) взято 20 точек на периоде]:
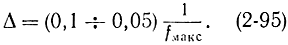
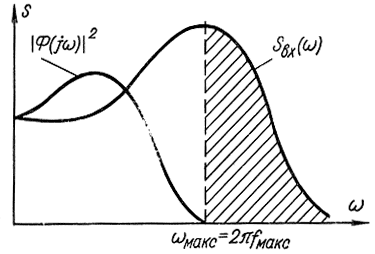
Рис. 2-6. Спектральная плоскость входного сигнала и квадрат модуля частотной характеристики системы (пояснения к расчету спектральной плоскости)
Пример 2-9. Для диагностики неисправности двигателя используется оценка корреляционной функции шума блока цилиндров. Необходимо определить параметры испытаний по определению этой оценки, т. е. найти τмакс, Т и Δ, если из кинематики двигателя известно, что исследуемая система пропускает шумы в диапазоне:
fмин=5 гц; fмакс=100 гц.
Используя эти данные, получаем:
ωмин=2πfмин=2*3,14*5≈31,5 рад/сек;
ωмакс=2πfмакс=2π*100≈628 рад/сек.
По формулам (2-91), (2-92) определяем:
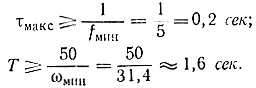
Шаг для 20 точек на период [формула (2-94)] равен:
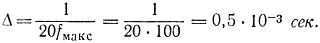
Если использовать пять или десять точек, то [формула (2-95)] имеем:
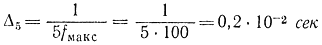
или
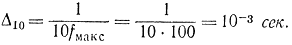
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'