б) Оценка спектральной плотности случайного стационарного процесса

Часто спектральная плотность стационарного случайного процесса определяется как

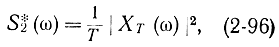
где

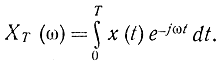
Найдем математическое ожидание оценки (2-96):

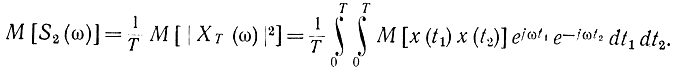
Вместо формулы (2-96) можно пользоваться выражением

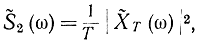
где

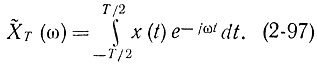
При этом все полученные ниже формулы остаются в силе для стационарного случайного процесса, так как

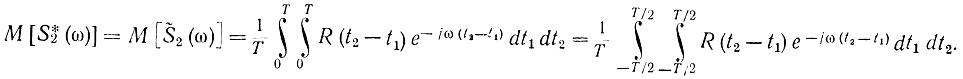
После замены переменных τ=t₂t₁ и преобразований, аналогичных тем, которые использовались при выводе формулы (2-82), имеем:

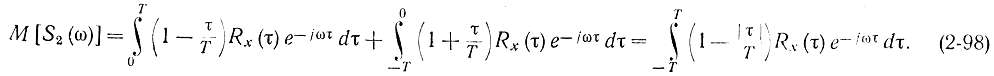
Переходя в этой формуле к пределу, получаем:

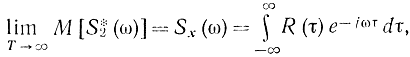
т. е. оценка спектральной плотности S*₂(ω) - асимптотически несмещенная, при Т→∞ (смещение этой оценки стремится к нулю при Т→∞ ). Таким образом, в части смещения оценка S*₂(ω) ведет себя нормальным образом. Однако в отношении дисперсии этой оценки положение неблагополучно, так как можно показать [Л. 20, 31, 32], что для нормальных процессов

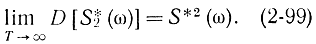
Если спектральную плотность оценивать по формуле

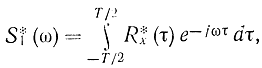
где

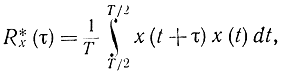
то из соотношения (2-99) следует, что

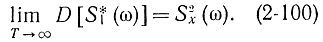
Действительно,

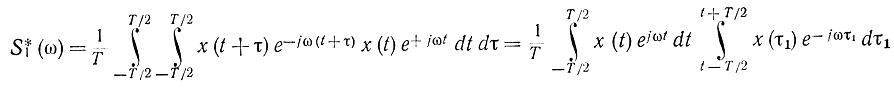
и при большом T

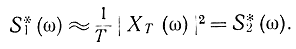
Отсюда следует, что по одной реализации стационарного случайного процесса можно определить корреляционную функцию, но нельзя определить спектральную плотность, так как дисперсия оценки S₂*(ω) при Т→∞ стремится к квадрату спектральной плотности S(ω), а не к нулю. Для определения спектральной плотности пользуются одним из трех способов. Самый простой способ состоит в том, что большой интервал наблюдения разбивают на n частей. Оценка спектральной плотности получается как среднеарифметическое оценок S*₂(ω) на всех отрезках. Дисперсия такой оценки будет равна:

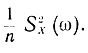
Ошибку определения спектральной плотности можно уменьшить, сглаживая оценку S*₂(ω) по частоте с помощью некоторой весовой функции ω_T(λ, ω):

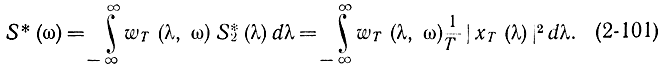
В качестве весовой можно взять функцию вида

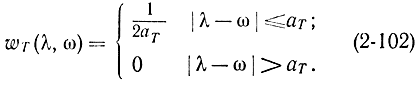
При выборе функции веса в виде (2-102) формулу (2-101) можно переписать как

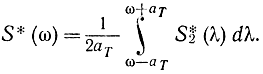
Физически это означает, что нас интересует только некоторый участок частот от λ-a_T до λ+a_T, в котором оценка должна быть точнее (вне этого интервала точность нас не интересует). Для выбора параметра ат вводят критерий оптимальности в виде минимума следующего выражения:

Первый член в последнем выражении представляет собой дисперсию самой оценки, а второе слагаемое - квадрат смещения оценки. При уменьшении величины параметра a_T полоса пропускания сглаживающего фильтра уменьшается, уменьшается дисперсия оценки, увеличивается ее смещение и поэтому имеется оптимальное значение параметра a_T.

Приведенный способ сглаживания оценки спектральной плотности S*₂(ω) тесно связан с теоремой Дуба [Л. 32], которая может быть записана с помощью соотношений:

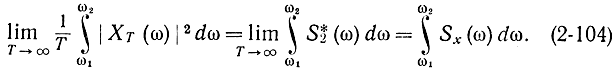
В этих формулах сходимость к пределу понимается в среднеквадратичном смысле, т. е. математическое ожидание квадрата отклонения от предела стремится к нулю при Т→∞ . Заметим, что хотя математическое ожидание оценки S*₂(ω) стремится к S_x(ω), математическое ожидание выражения [S*₂(ω)-S_x(ω)]² не стремится к нулю. Если правую часть равенства (2-104) поделить на ω₂-ω₁ и устремить ω₂-ω₁ к 0, получится спектральная плотность процесса S_x(ω). В левой части такого перехода сделать нельзя, так как _TХ при Т→∞ является белым шумом и, следовательно, на любом сколь угодно малом интервале (ω₁,ω₂) совершает бесконечное множество скачков (предел можно брать, если он существует).

По существу теорема Дуба доказывает, что несмотря на то, что оценка спектральной плотности не стремится в среднеквадратичном смысле к самой спектральной плотности, интеграл от этой оценки стремится в среднеквадратичном смысле к интегралу от спектральной плотности.

Если не решать строго задачу оптимального выбора ат по критерию, задаваемому формулой (2-104), то можно дать следующие, не очень строго обоснованные рекомендации по выбору этой величины. С одной стороны, при данном Т оценка (2-101) тем лучше, чем больше a_T, так как тем лучше будет сглаживание, однако, с другой стороны, функция S*₂(ω) должна в интервале (ω-a_T, ω+a_T) быть линейной функцией частоты ω, или она должна быть постоянной в этом интервале, для того чтобы получить менее искаженное сглаживающим фильтром и не зависящее от a_T значение оценки S*₂:

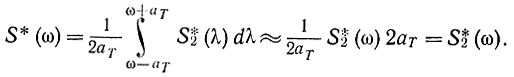
С помощью формул (2-101) и (2-103) можно предложить следующий способ экспериментального определения спектральной плотности стационарного случайного процесса по одной реализации. Случайный процесс пропускается через полосовой фильтр (ω-a_T, ω+a_T), и в течение долгого времени измеряется его мощность или дисперсия (при этом предполагается, что процесс имеет нулевое математическое ожидание). Тогда спектральная плотность определится как

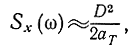
где D - дисперсия; 2a_T - полоса фильтра. На основании этого иногда применяется процедура сглаживания не оценки спектральной плотности, а самой реализации или оценки корреляционной функции [Л. 32], которая также дает желаемый результат.

Наиболее распространен на практике следующий способ определения спектральной плотности. С помощью формул (2-84) и (2-85) вычисляют корреляционную функцию по одной реализации. Затем ее аппроксимируют по методу наименьших квадратов выражением вида

или комбинацией таких выражений. После этого берут преобразования Фурье от аппроксимирующего аналитического выражения. Иногда наряду с (2-105) используют в аппроксимирующем выражении еще слагаемые вида

Оказывается, корреляционную функцию реального стационарного процесса в большинстве случаев можно представить как сумму выражений вида (2-105) и (2-106). Спектральная плотность такого процесса будет иметь вид дробно-рациональной функции [Л. 27]. На этом способе следует подробнее остановиться. Выше было получено

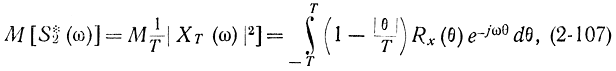
откуда в пределе

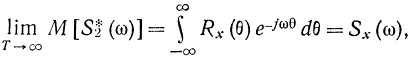
на основании чего делалось заключение о не смещенности оценки S*₂(ω). С другой стороны, можно получить:

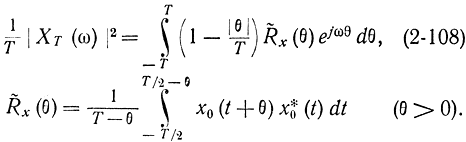
Таким образом, если известно точное выражение для корреляционной функции, то преобразование Фурье от нее дает искомую спектральную плотность. Однако непосредственное определение спектральной плотности по одной реализации (без применения усреднения или сглаживания) или по оценке корреляционной функции, вычисленной по одной реализации, которая задана на конечно интервале, невозможно согласно формуле (2-108). Если не применять первый и второй способы, то единственная возможность определить спектральную плотность - это точнее вычислить корреляционную функцию, для чего можно применить усреднение по ансамблю. Введение процедуры аппроксимации оценки корреляционной функции, вычисленной по одной реализации, предусматривает угадывание точного выражения для корреляционной функции. Это аппроксимирующее выражение тем ближе к истинной корреляционной функции, чем больше интервал наблюдения Т, чем точнее вычислена оценка функции R(ω), чем точнее произведена процедура подбора аппроксимирующего выражения. Корректность третьего способа определения спектральной плотности требует специального исследования, так как, с одной стороны, аппроксимации подвергается все та же оценка корреляционной функции на конечном интервале по одной реализации, но, с другой стороны, процедура аппроксимации при достаточно большом интервале Т безусловно, позволяет угадать достаточно точное аналитическое выражение для корреляционной функции.

По существу процедура аппроксимации корреляционной функции эквивалентна сглаживанию ее оценки, которое эквивалентно сглаживанию оценки спектральной функции по формуле (2-101), только для этого следует взять весовую функцию k_T(λ,t), "равную обратному преобразованию Фурье от функции w_T(λ,ω). Первый способ определения спектральной плотности путем разбиения реализации на n интервалов тоже эквивалентен взвешиванию оценки S*₂(ω) с помощью специальной функции w_T(λ,ω).