2-6. Элементы статистического анализа совокупности случайных величин

Две случайные величины X и Y связаны детерминированной функциональной зависимостью

если каждому допустимому значению х соответствует одно (в случае однозначной функции) значение у [Л. 331.Если функция неоднозначна, то конкретному значению X всегда можно сопоставить ряд (конечный или бесконечный) вполне определенных значений Y. В качестве при-мера можно привести следующие функции:

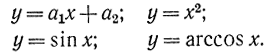
Преобразования случайной величины рассматриваются в теории вероятности. При этом интересуются изменением в различных функциональных преобразованиях характеристик случайной величины X: функции распределения, моментов и пр. Однако в практических исследованиях возникают другие специфические задачи. Детерминированная функциональная зависимость практически встречается редко или, строго говоря, совершенно отсутствует, так как при измерениях величин X и Y всегда имеются ошибки и влияние случайных, не учитываемых факторов. Причем каждая из величин X и Y может зависеть от одних и тех же и от различных случайных факторов. Так, X может зависеть от случайных величин Z₁, Z₂, V₁, V₂, a Y от Z₁ и Z₂. В этом случае влияющие факторы Z₁ и Z₂ общие, остальные разные, что может иметь место в случае, когда измерительные устройства для X и Y разные или когда эти величины имеют различную природу, например X - электрическая величина (ток), a Y - механическое перемещение. В этом случае связь двух случайных величин становится статистической (случайной) в том смысле, что по данному значению X нельзя получить определенное значение Y, так как это последнее зависит помимо X еще от случайных факторов V₁и V₂.

В общем случае (как и в данном частном) можно считать, что Y зависит от X случайным образом и эту зависимость можно определить с помощью известных из теории вероятности характеристик многих случайных величин, таких как совместное распределение вероятности, условная плотность распределения, коэффициенты корреляции, моменты и пр.

Существует непрерывный переход от строгой детерминированной функциональной зависимости через статистическую зависимость к полностью независимым случайным величинам. Приведем несколько примеров. Состояние погоды Y (ясно или пасмурно) в данной местности существенным образом зависит от атмосферного давления X. При низком давлении погода пасмурная, при высоком - ясная. Предсказание погоды зависит от изменения давления: при повышении она улучшается, при понижении ухудшается. Однако наряду с такой детерминированной функциональной зависимостью имеется большое количество факторов, от которых зависит погода на последующие сутки или неделю: давление в соседних районах, температура, направление и сила ветра и пр. Часть этих факторов поддается учету, остальные приходится считать случайными, так же как и зависимость от них. Таким образом, зависимость погоды на следующие сутки от изменения давления за предыдущие сутки носит в общим случае статистический характер.

Можно привести еще пример из области сельского хозяйства. Урожай зерна Y существенно зависит от количества вносимых удобрений X. Однако, помимо того, урожай зависит еще от многих факторов: состава и состояния почвы, семян, погоды и пр. Поэтому зависимость величин X и Y носит статистический характер.

Не очень строго статистическая связь может быть определена как такая зависимость, при которой изменение значения одной величины X вызывает изменение закона распределения (а не значения) другой величины Y. Если при статистической зависимости изменение одной величины приводит к изменению среднего значения другой, то такая связь называется корреляционной. В двух приведенных примерах средние значения величин Y (погода и урожай) детерминированно зависят от значений X (изменения давления и количества удобрений). При корреляционной зависимости для определения статистической связи достаточно задать корреляционные моменты. Это простейший частный случай статистической зависимости, при которой следует задавать законы совместного распределения случайных величин X и Y.

Данный раздел, с одной стороны, связан и перекрывается с теорией оценок, так как речь пойдет об оценке и достоверности тех или иных параметров связи, и, с другой стороны, переходит в теорию проверки статистических гипотез, основной целью которого является определение законов распределения одной случайной величины или их совокупности по результатам измерений.

На практике встречается много частных постановок задач установления статистической связи. Так, часто встречается вид функциональной связи (линейная, квадратичная и пр.), и требуется определить только числовые значения параметров этой зависимости по полученным в результате эксперимента значениям X и Y. Иногда при этом путем последовательных проб подбирается и наилучший вид детерминированной функциональной зависимости (линейная или квадратичная). С такой задачей мы встречались при аппроксимации расчетной корреляционной функции аналитическим выражением. Наиболее распространенным и эффективным способом решения этой задачи является метод наименьших квадратов, который будет рассмотрен в данном параграфе. В более общем случае о связи двух случайных величин ничего не известно, и требуется определить на уровне корреляционных моментов степень их зависимости. Корреляционному анализу посвящен второй раздел данного параграфа. Более совершенные и сложные методы установления статистической связи, в частности определение взаимных законов распределения, будут рассмотрены в следующей главе, посвященной проверке статистических гипотез.

В последнее время в результате решения задач анализа статистической связи случайных величин появился новый раздел математической статистики - планирование эксперимента, который занимается исследованием методов организации сбора и измерения значений случайных величин для установления статистической зависимости.