а) Метод наименьших квадратов
Допустим, что имеется совокупность двух случайных величин X и Y и известен вид функциональной зависимости между ними: y=φ(x). На миллиметровой бумаге откладывают точки, соответствующие измеренным значениям х и y (рис. 2-7). Требуется провести через эти точки кривую наилучшим образом [Л. 21] Понятие "лучшее" математически может быть выражено различным способом. Проводить непосредственно через точки неправильно, так как очевидно, что разброс вызван ошибками измерений. Например, можно потребовать чтобы сумма абсолютных значений расстояний точек от кривой была минимальна или максимальное отклонение было минимальным и пр. Но наиболее распространенным критерием оптимальности является минимум суммы квадратов отклонений
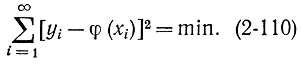
Критерий минимума суммы квадратов часто применяется по трем соображениям. Во-первых, при этом большое количество задач оказывается возможным решить аналитически. Во-вторых, при квадратичной зависимости получается, что ущерб (сожаление) при малых значениях ошибок мал, а с их увеличением резко возрастает. Это обстоятельство правильно отражает практическую ситуацию, так как малые ошибки менее опасны, чем большие. И, наконец, при этом критерии удовлетворяется критерий максимума правдоподобия для случая, когда отклонения подчиняются нормальному закону распределения.
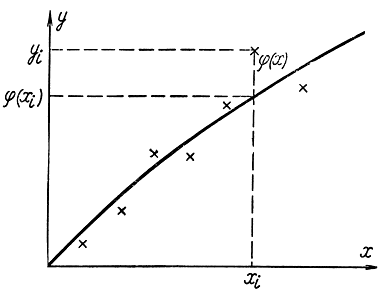
Рис. 2-7. Пояснения к процессу сглаживания случайных данных
Задачу будем решать при условии, что известен вид функции и требуется найти только числовое значение параметров. В частности, зависимость y=φ(x) может быть задана прямой линией
y=ax+b
или параболой
y=ax2+bx+c
или функциями вида (2-107) и (2-108) при вычислении корреляционной функции. Допустим, что сделано n замеров величин Xi и Yi. Предположим, что среднеквадратичные ошибки измерения во всех точках одинаковы: σ1=σ2=...=σn=σ и распределены по нормальному закону. Тогда величины Yi подчиняются нормальному закону распределения
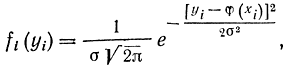
где φ(xi) - математическое ожидание величин Yi.
Принцип максимального правдоподобия применительно к этой задаче может быть сформулирован следующим образом: требуется так подобрать математическое ожидание φ(xi), чтобы вероятность события, состоящего в том, чтобы величины Yi приняли значение yi была максимальна. Такая постановка задачи о сглаживании по методу наименьших квадратов фактически заимствована из раздела проверки статистических гипотез. Строго говоря, вероятность любых событий Yi=yi как и их произведения, равна нулю, так как случайные величины Yi непрерывные. Поэтому следует пользоваться плотностью распределения вероятности или элементами вероятности
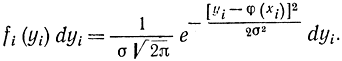
Найдем вероятность того, что случайные величины Y1, Y2, ..., Yn лежат в пределах:
(yi,yi+dyi), i=1,2...,n
Считаем, что опыты независимы, поэтому искомая вероятность равна произведению вероятностей
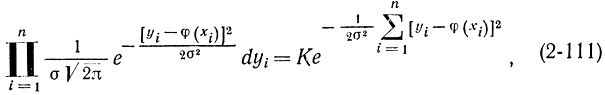
где К- некоторый коэффициент, не зависящий от φ(xi). Необходимо выбрать такие математические ожидания φ(xi). , чтобы функция (2-111) обращалась в максимум. В этом и заключается принцип максимального правдоподобия. Очевидно, что величина
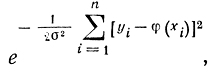
меньшая единицы, будет иметь наибольшее значение, когда показатель степени по абсолютной величине минимален, т. е.
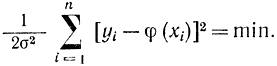
Отсюда, отбросив множитель 1/2σ2, получим условие минимума суммы квадратов, задаваемое формулой (2-110), т. е. доказано, что для случая независимых измерений, которые подчиняются нормальному закону распределения, принцип максимума правдоподобия совпадает с методом наименьших квадратов.
Дадим практические методы определения параметров кривой при методе наименьших квадратов. Допустим, что функция φ(x). зависит от m переменных a1, a2,...,am
y=φ(x,a1,a2,...,am)
Требуется найти такие значения aν, чтобы
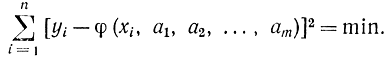
Для этого продифференцируем это выражение по aν и приравняем нулю
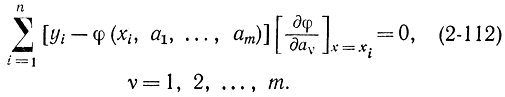
ν=1,2,...m
Уравнения (2-112) представляют собой систему m нелинейных алгебраических уравнений с m неизвестными aν. Решать эту систему в общем виде нельзя, так как требуется задание функции φ(a1,a2,...am). В качестве примера найдем выражения для коэффициентов линейной функции:
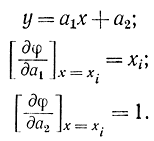
Подставив их в формулу (2-112)
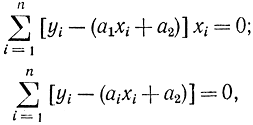
и деля оба уравнения на n, запишем:
a*1,1[X,Y]-a1a2*[X]-a2m*x=0
m*y-a1m*x-a2=0
где
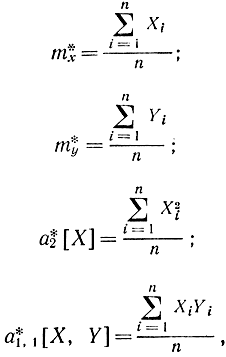
и решив их, получим:
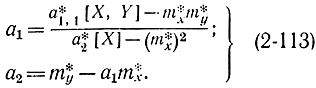
Формулы значительно упростятся, если ввести центральные моменты
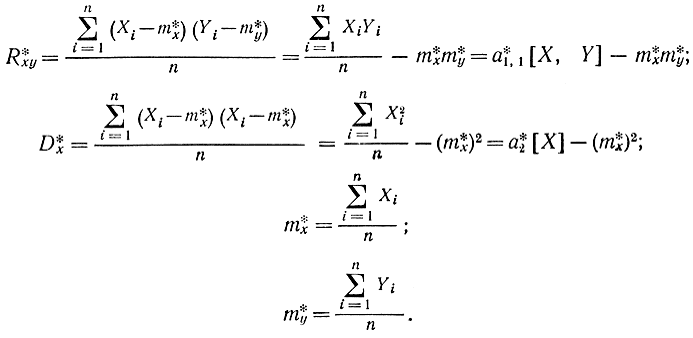
Тогда
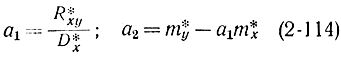
или
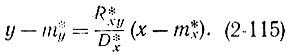
Аналогичным образом могут быть получены значения для параболической функции.
Пример 2-10. В результате эксперимента получены значения X и Y (табл. 2-4) и можно составить табл. 2-5.

Таблица 2-4
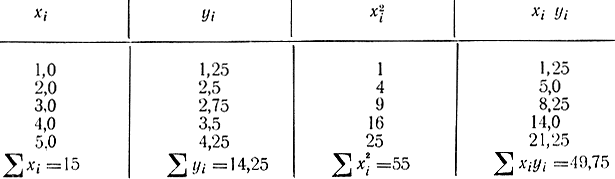
Таблица 2-5
С помощью формул (2-114) получим:
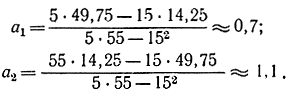
Линейная функция запишется в виде
y=0,7x+1,1
Пользуясь табл. 2-6, определим сумму квадратов отклонений для этого выражения.
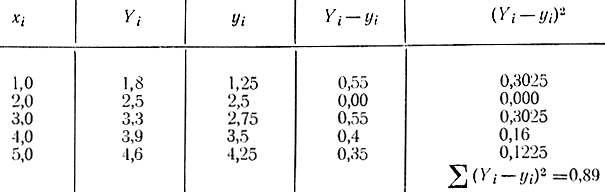
Таблица 2-6
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'