б) Элементы корреляционного и регрессионного анализа

Для определения корреляционной зависимости между случайными величинами X и Y необходимо использовать понятие условных средних [Л. 33]. Условным средним

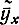
называется среднеарифметическое значений Y, соответствующих X=х. Очевидно, что при увеличении числа опытов условная средняя стремится к условному математическому ожиданию

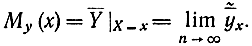
Если при значении x=3, Y принимает значения y₁=7, y₂=3, y₃=8, то условная средняя

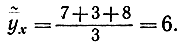
Корреляционной зависимостью Y от X называется функциональная зависимость ȳ_x от x:

Это уравнение называется уравнением регрессии Y на X, функция φ(x) - регрессией Y на X, а ее графическое изображение φ(x)- линией регрессии Y на X. Аналогичным образом определяют регрессию X на Y. Корреляционной зависимостью X от Y называется функциональная зависимость условной средней x_y от y:

Обычно отмечают две задачи корреляционного анализа. В первом случае определяют вид корреляционной зависимости: линейный, квадратичный, синусоидальный и пр. Во втором случае определяют степень (силу) корреляционной связи, которая оценивается по величине рассеивания точек относительно линии регрессии. Теснота группирования точек около линии регрессии чаще всего оценивается с помощью суммы средних квадратов. Причем степень корреляционной связи может оцениваться как Y относительно X, так и X относительно Y, которые в общем случае не совпадают.

Рассмотрим вначале простейший случай отыскания выборочного уравнения прямой линии регрессии по не сгруппированным данным. При этом предполагается, что величины X и Y связаны линейной корреляционной зависимостью. Для определения этой зависимости произведено n независимых испытаний и получено n пар значений:

Так как эти пары представляют собою случайную выборку из совокупности всех возможных значений векторной случайной величины (X, Y), которая называется генеральной совокупностью, то все уравнения и параметры, которые получаются на основании этих данных, называются выборочными. Будем считать, что различные значения х признака (величины) X и соответствующие им значения y признака Y встречаются по одному разу. В этом случае не требуется группировать данные, а также использовать понятие "условное среднее". Искомое уравнение регрессии

можно переписать в виде

Угловой коэффициент прямой регрессии Y на X называется выборочным коэффициентом регрессии Y на и X обозначается через ρ_yx

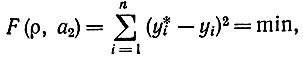
Если подбирать параметры ρ_xy условия минимума суммы квадратов отклонений измеренных значений y_i от вычисленных по формуле прямолинейной регрессии

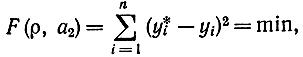
то для величин ρ_xy и a₂ получим формулы, аналогичные тем, которые были получены в методе наименьших квадратов для прямолинейной зависимости (2-114). В данном случае

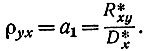
При большом числе измерений и ярко выраженной статистической связи ситуация становится сложнее: одно и то же значение x_i может появляться nx_i раз, так же как и одно значение y_i может встречаться ny_i раз, а пара значений x_i и y_i может встретиться nx_iy_i раз. Поэтому при корреляционном анализе составляется корреляционная таблица (табл. 2-7).

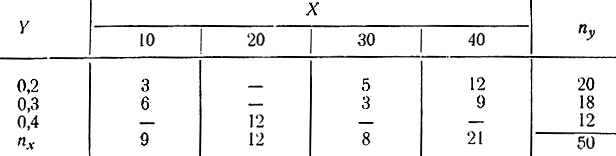
Таблица 2-7

В каждой внутренней клетке указывается число наблюдений соответствующих признаков, на пересечении которых расположена клетка. В первой строке указываются значения признака X, в первом столбце - значения признака Y. В правом нижнем углу указано общее число испытаний n=∑n_x=∑n_y.

Получим для этого случая уравнение регрессии с учетом частоты появления признаков. В предыдущем разделе были получены соотношения, определяющие уравнение регрессии, которое можно переписать в виде

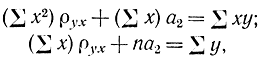
где для простоты опущены индексы суммирования, так как везде предполагается, что суммирование производится по индексу i или j или i и j в пределах от 1 до n. При выводе этих соотношений считалось, что значения X и Y встречаются по одному разу. Учтем в этих уравнениях то, что признаки появляются несколько раз и имеется корреляционная таблица. Если использовать соотношения для средневзвешенных значений

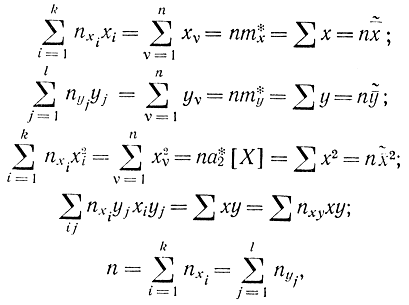
в которых учтены частоты появления признаков x_i, y_i, то соотношения, которые определяют уравнение регрессии, перепишутся в виде

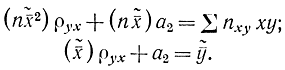
Отсюда можно найти параметры ρ_yx и a₂ и написать уравнение регрессии

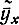=ρ_yxx+a₂

Аналогично соотношению (2-115) это уравнение можно переписать в виде

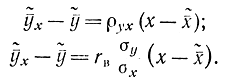
Это уравнение называется выборочным уравнением регрессии Y ка X. Коэффициент r_в называется выборочным коэффициентом корреляции и определяется как

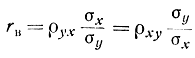
или

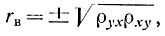
где в соответствии с ранее приведенным

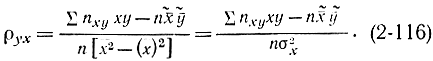
Поэтому

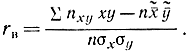
Здесь σ_x и σ_y - выборочные среднеквадратичные отклонения, определяемые из соотношений:

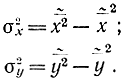
Аналогичным образом можно написать выборочное уравнение прямой регрессии X на Y

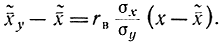
Оба уравнения прямых могут быть записаны в следующем симметричном виде:

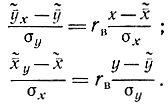
Оказывается, величина выборочного коэффициента корреляции указывает на степень линейной корреляционной зависимости, на степень тесноты этой зависимости. Степени линейных корреляционных зависимостей Y от X и X от Y могут быть оценены с помощью величин соответствующих дисперсий S_y и S_x наблюденных значений y их вокруг их условных средних 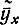и

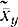
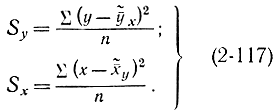
Можно показать, что

где D_y=σ²_y и D_x=σ²_x - дисперсии наблюденных значений y и x относительно средних 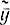и .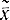

Можно показать, что абсолютное значение выборочного коэффициента корреляции не превышает единицы в силу того, что любая дисперсия неотрицательна, т. е.

и поэтому

При нулевом выборочном коэффициенте корреляции и прямых линиях регрессии значения признаков X и Y в выборке не связаны линейной корреляционной зависимостью. Действительно, при r_вО уравнения выборочных прямых регрессии Y на X имеют вид:

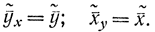
Это означает, что при изменении соответствующей величины условные средние не изменяются и остаются равными соответствующим средним, т. е. зависимость Y от X, как X от Y, отсутствует. В данном случае прямые регрессии параллельны координатным осям. Однако следует заметить, что при нулевом выборочном коэффициенте корреляции величины X и Y могут быть связаны нелинейной статистической и детерминированной зависимостью. Наоборот, при единичном значении абсолютной величины выборочного коэффициента корреляции значения признаков Y и X в выборке связаны линейной детерминированной зависимостью. Действительно, если

то

и, следовательно,

или

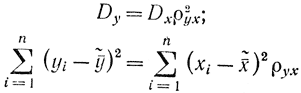
или

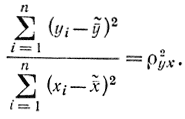
Это соотношение может в общем случае удовлетворяться при условии, если

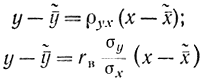
(что можно доказать методом от противного). Но последние соотношения показывают, что любые случайные значения X и Y лежат на прямой, т. е. значения признаков в выборке связаны детерминированной линейной зависимостью.

Из приведенных свойств выборочного коэффициента корреляции следует, что с возрастанием его по абсолютной величине корреляционная зависимость становится более тесной, так как в соответствии с формулами

дисперсии S_y и S_x убывают. Тем самым показано, что этот коэффициент характеризует тесноту связи.

Все предыдущие суждения были основаны на данных определенной выборки, которая в зависимости от своего объема может с той или иной полнотой представлять генеральную совокупность. В связи с этим всегда надо быть осторожным при распространении выводов о выборке на всю генеральную совокупность, но определенные суждения сделать можно, особенно при большом объеме выборки. Так, для n≥50 в случае нормально распределенной генеральной совокупности [Л. 33] выборочный коэффициент корреляции r_в связан с генеральным коэффициентом корреляции r_г соотношением

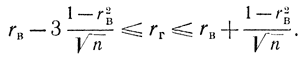
Пример 2-11. Для числовых значений, приведенных в табл. 2-5, требуется вычислить выборочный коэффициент корреляции r_в. Вычисляем выборочный коэффициент регрессии по формуле

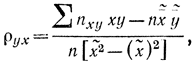
причем

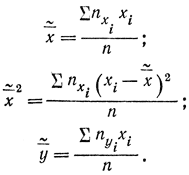
В результате получим:

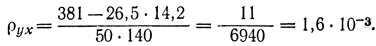
Отсюда в соответствии с формулой

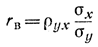
имеем:

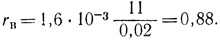
Из полученного видно, что данная выборка обладает достаточно большой корреляционной связью, хотя числа в корреляционной таблице задавались произвольно. Наконец, используя формулы

можем вычислить дисперсию относительно линий регрессии

Такое различие в дисперсиях вызвано различным порядком величин X и Y, которые отличаются примерно на 10².