в) Энтропия непрерывных сообщений

Прежде всего энтропию непрерывных сообщений можно ввести сведением непрерывных сообщений к дискретным с помощью теоремы Котельникова. Однако имеется и другой способ, о котором речь пойдет ниже. Строго говоря, энтропия непрерывных сообщений равна бесконечности, так как бесконечны количество возможных сообщений (мы имеем дело с континуумом), его логарифм и неопределенность выбора значений случайной величины.

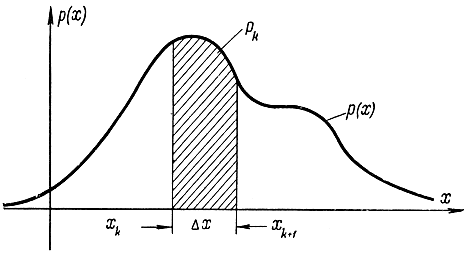
Рис. 6-1. Замена непрерывного сообщения соответствующим дискретным

В случае непрерывных сообщений роль функции распределения их вероятности играет плотность распределения вероятности р(х). Можно считать, что эта функция, так же как величина х, безразмерна: всегда можно свести размерную величину х к безразмерной x, поделив ее на масштабный множитель х₀, т. е.

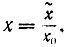
Заменим непрерывное сообщение соответствующим дискретным, введя процесс квантования (рис. 6-1). Дискретная квантованная величина характеризуется распределением, в котором вероятность k-го состояния определяется как

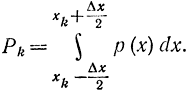
При стремлении Δx в пределе к нулю получим исходный непрерывный сигнал. Поэтому рассмотрим энтропию этого квантованного сигнала, которая, очевидно, будет зависеть от Δx, после чего устремим Δx к нулю и получим искомое выражение для энтропии непрерывного сигнала:

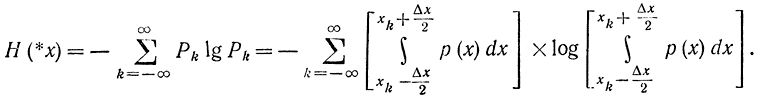
При достаточно малой Δx и гладкой функции р(x) можно считать, что

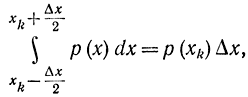
поэтому

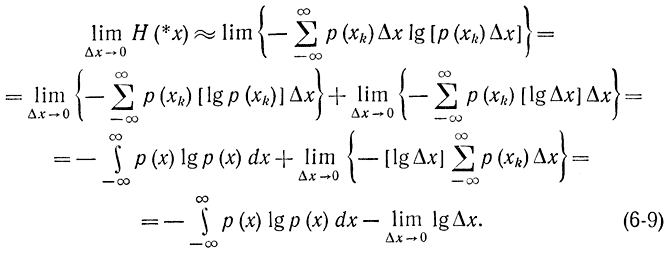
Как и следовало ожидать, энтропия квантованного сигнала стремится к бесконечности при Δx→0.

Таким образом, непрерывные сигналы-сообщения не имеют абсолютной меры энтропии. Поэтому для них вводят понятие относительной энтропии (неопределенности). В качестве эталона чаще всего выбирается непрерывный сигнал х', имеющий равномерный закон распределения в интервале ε. Формула (6-9) для такого сигнала перепишется в виде

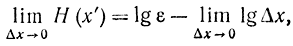
так как

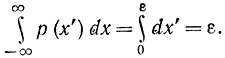
Неопределенность непрерывной величины x характеризуется числом, к которому стремится разность энтропий сигналов *x и х':

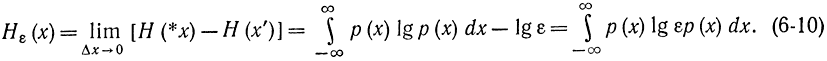
Если положить ε=1 (т. е. стандартная величина имеет равномерный закон распределения в единичном интервале), то формула (6-10) перепишется в виде

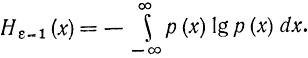
Это выражение не означает, что получена абсолютная мера энтропии непрерывного сигнала. Следует помнить, что это - относительная энтропия, где за стандарт взята равномерно распределенная в единичном интервале величина. Иногда величину Н_ε=1(х) называют дифференциальной ε-энтропией и часто опускают индекс ε=1.