г) Экстремальные свойства энтропии непрерывных сообщений

Представляет интерес решение следующей задачи. Задан какой-то ансамбль сообщений или сигналов, о котором известны некоторые параметры. Например, пределы изменения, дисперсия, математическое ожидание. Требуется подобрать такой закон распределения этого ансамбля, при котором энтропия была бы максимальной. Можно дать две физические интерпретации принципа максимальной энтропии. К примеру, требуется создать помеху каналу связи противника, чтобы создать в нем максимум неопределенности. Очевидно, что наилучший эффект будет достигнут при заданных параметрах, если будет выбран такой закон распределения помехи, при котором энтропия принимает максимальное значение.

Второй пример можно привести из области задач, которые в математической статистике объединяются под названием "критерии согласия". На практике очень часто встает задача подбора наилучшего в известном смысле закона распределения случайного сигнала, о котором известны некоторые данные, упоминавшиеся выше. В данном случае предлагается критерий максимальной энтропии. В этом случае гарантируется отсутствие субъективизма, так как из всех законов, которые обладают заданными параметрами, выбран такой, который обеспечивает максимум неопределенности.

Первый случай. Рассмотрим ограниченную на интервале [а, b] непрерывную случайную величину с неизвестной плотностью распределения р(х), причем

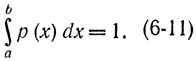
Требуется найти аналитическое выражение для функции р(х), которое дает максимум энтропии, задаваемой выражением

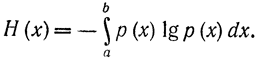
Согласно вариационному исчислению в соответствии с формализмом Лагранжа -Эйлера необходимо составить дифференциальное уравнение Эйлера относительно подынтегральной функции F(х, р), входящей в функционал, который подлежит минимизации

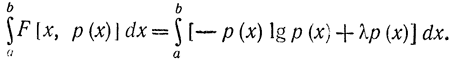
Соответствующее уравнение Эйлера может быть записано в виде

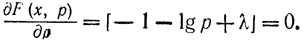
Отсюда

Используя соотношение (6-11), получаем уравнение для определения неизвестной постоянной к в виде

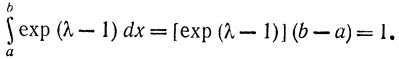
Поэтому

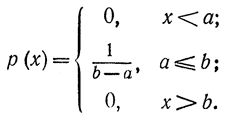
Тем самым получено уже известное положение, что для ограниченной на конечном отрезке случайной величины максимальная энтропия получается при равномерном распределении (факт, известный для случая дискретных сообщений). Очевидно, это свойство является некоторым оправданием для выбора в качестве эталонного сообщения при введении дифференциальной энтропии, имеющего равномерный закон распределения в интервале квантования ε.

Второй случай. Будем считать, что область изменения случайной величины неограниченна: -∞≤х≤∞, задано среднее значение х=а и дисперсия 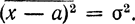. Требуется найти закон распределения р(х), при котором функционал, равный энтропии, обращается в максимум

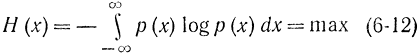
при условиях

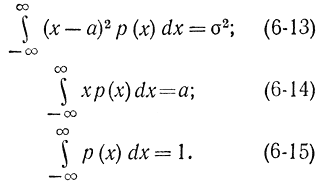
Вводя неопределенные множители Лагранжа λ₁, λ₂, λ₃ получим уравнение для определения искомой функции р(λ) в виде

откуда

Используя условие (6-15), получаем:

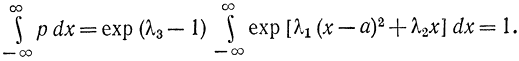
Из этого соотношения следует, что для сходимости интеграла переменная λ₁ должна быть отрицательная. Поэтому, используя таблицы интегралов [Л. 55], получаем:

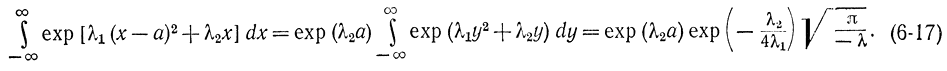
Отсюда

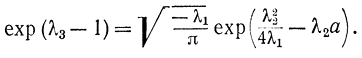
Соотношение (6-13) с использованием (6-16) и (6-17) после несложных преобразований примет вид:

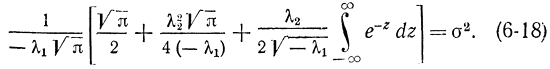
Для ограниченности левой части этого соотношения λ₂=0. Поэтому

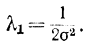
Окончательно соотношение (6-16) запишется в виде

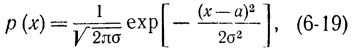
т. е. экстремальное распределение является нормальным распределением.

Аналогичным образом можно показать, что для случайной величины х, ограниченной положительной полуосью 0 ≤х≤+∞, экстремальным распределением будет экспоненциальное распределение

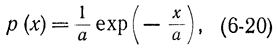
где а - математическое ожидание х.