д) Энтропийная мощность непрерывных сообщений

Покажем, что дифференциальная энтропия белого нормального шума при ε=1 на один отсчет определяется по формуле

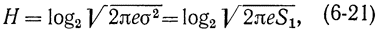
где ε - основание натуральных логарифмов; σ² - дисперсия белого шума; S₁=σ² - средняя мощность белого шума на единичную полосу. Считается, что для белого шума σ²=S₁f_c.

Один отсчет понимается таким образом, что непрерывный по времени сигнал заменяется дискретным по времени сигналом с интервалом дискретности, определяемым в соответствии с теоремой Котельникова:

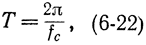
где f_c - ширина спектра непрерывного сигнала (амплитудами составляющих сигнала, имеющими частоты выше этой частоты, можно пренебречь), т. е. заменяем непрерывный сигнал с шириной полосы f_c на интервале t₀ дискретными значениями, число которых подсчитывается по формуле Котельникова:

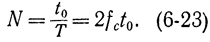
Докажем формулу (6-21). Для нормального сигнала х плотность распределения вероятности определяется по формуле

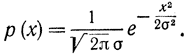
Отсюда, логарифмируя, получаем:

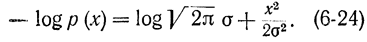
По определению энтропии непрерывных сообщений (а точнее, дифференциальной энтропии при ε=1) имеем:

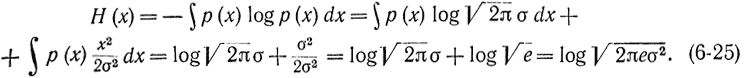
Тем самым формула (6-21) доказана. В соотношениях (6-25) использована формула (6-24) и следующая формула, определяющая дисперсию:

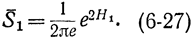
По теореме Котельникова [формула (6-23)] среднее число отсчетов или степеней свободы сигнала с шириной спектра составляет 2f_c в 1 сек. Поэтому энтропия рассматриваемого сигнала на единицу времени равна:

Энтропийная мощность S^-₁ произвольного случайного сигнала, имеющего ширину спектра f_c и энтропию Н₁ определяется как средняя мощность белого нормального шума с такой же полосой пропускания и с такой же энтропией на степень свободы, т. е.

Здесь просто перевернуто выражение (6-21), т. е. хотя процесс не имеет нормального распределения, заменяем его эквивалентным сигналом (с нормальным законом) и считаем, что справедливо соотношение (6-21).

Рассмотрим некоторые свойства энтропийной мощности. Энтропийная мощность S^-₁ случайного сигнала с произвольным законом распределения не превышает его действительной средней мощности S₁ т. е. S^-₁≤S₁, так как при заданной средней мощности (дисперсии) нормальный процесс обладает максимальной энтропией, если этот процесс х изменяется от - ∞ до +∞. Пусть n₁ - сигнал с нормальным законом распределения, а n - сигнал с произвольным законом распределения при

Требуется доказать, что если

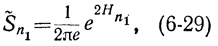
то

Это соотношение следует из того, что нормальный процесс обладает максимальной энтропией.

Это положение позволяет брать в качестве верхней границы энтропийной мощности действительную мощность сигнала, когда неизвестно распределение этого сигнала.

Докажем очень важную формулу для энтропийной мощности не белого нормального шума через его спектральную плотность мощности S(f):

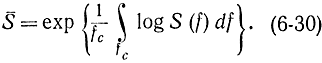
Для доказательства будем считать функцию S(f) дифференцируемой, за исключением конечного числа точек. Разобьем весь интервал частот (0, f) на узкие полоски df, в пределах которых можно считать спектральную плотность постоянной величиной. Будем считать, что исходный процесс состоит из суммы сигналов белых шумов, имеющих в интервале (f_сf+df) значение средней мощности S(f), Величина энтропии на единицу времени для такого процесса равна:

Будем считать, что все эти сигналы независимы друг от друга. Это положение, конечно, требует своего обоснования. Тогда энтропия сигнала равна сумме энтропии:

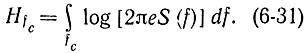
Учитывая, что среднее число степеней свободы процесса с шириной полосы f_c равно 1/2f_с, получаем, что энтропия сигнала на одну степень свободы равна:

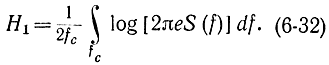
Очевидно, что энтропийная мощность в соответствии с формулами (6-32) и (6-27) может быть записана в виде (6-30). Действительно,

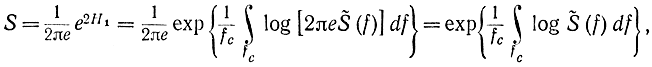
что и требовалось доказать.