е) Изменение дифференциальной энтропии при линейной фильтрации

Допустим, что на вход фильтра с частотной характеристикой Y(f) подается случайный сигнал х(f). Известно [Л. 28], что спектральные плотности входного и выходного сигналов связаны соотношением

где Y(f) - частотная характеристика фильтра; S_х(f) и S_y(f) - спектральные плотности мощности входного и выходного сигналов. Для энтропии на единицу степени свободы получаем:

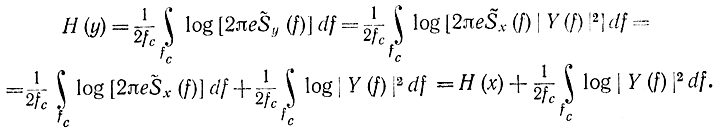
Отсюда изменение энтропии на степень свободы при прохождении через фильтр

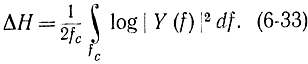
Полученная формула предполагает нормальные законы распределения вероятностей входного и выходного сигналов. Из формулы (6-33) следует, что для фильтра из пассивных элементов |Y (f)|≤1 и ΔН≤0 (рис. 6-2, а), поэтому говорят о потерях информации в линейных фильтрах. Если линейный фильтр содержит усилительные элементы (рис. 6-2, б), то энтропия сигнала может как уменьшаться, так и увеличиваться или оставаться неизменной.

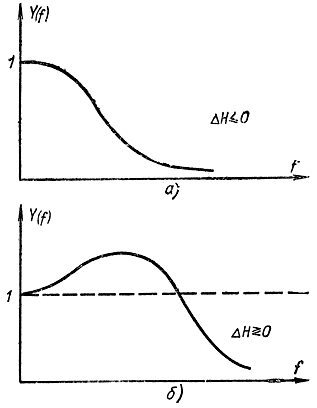
Рис. 6-2. Изменение энтропии сигнала при прохождении через фильтр