Глава седьмая. Передача сообщений по каналу связи

7-1. Понятие относительной информации

Следует заметить, что различие между количеством информации и энтропией в ряде случаев носит условный характер. Так, если рассматривать энтропию всех возможных сообщений длиной n, то эта величина будет совпадать с количеством информации, задаваемой формулой (6-3). И наоборот, если нас интересует информация на один символ, содержащаяся в ансамбле сообщений, то эта величина определяется величиной энтропии этого ансамбля. При передаче сообщений необходимо дать математическую формулировку данного в начале второй части определения количества информации как меры снятия неопределенности, которая численно равна разности априорной и апостериорной энтропии принимаемого сигнала:

где H - априорная, Н₀ - апостериорная энтропии. При этом определении, которое иногда называется третьим определением количества информации (имея в виду, что первое - по Хартли, второе - по Шеннону), считается, что информация относится к одному символу сообщения или энтропия-к определенной длине n сообщения. Это определение одинаково справедливо для дискретных и непрерывных сообщений. В последнем случае вообще трудно установить существенную разницу между количеством информации и энтропией. Если обозначить через

Н(х) - энтропию множества передаваемых символов (на входе канала связи);

Н(y) - энтропию множества принимаемых символов;

Н(х,y) - энтропию множества всевозможных пар (x_i, y_k);

H(x|y) - энтропию множества отправляемых символов, оставшуюся после приема символа y_k;

H(y|x_k) - энтропию множества принимаемых символов при условии, что известен отправленный символ;

H(х|y) и H(y|x) - математические ожидания величин Н(x|y_k) и Н(y|x_k), то в соответствии с формулой (7-1) количество информации при приеме символа y_k определяется по формуле

Очевидно, что величина I_k является случайной, и необходимо ее усреднить по всему множеству принимаемых символов, так же как это было сделано при выводе формулы (6-4):

Учитывая свойства взаимной плотности распределения вероятностей двух случайных величин [Л. 21], нетрудно убедиться в справедливости формулы

или

Подставив это выражение в формулу (7-2), получим:

Формулы (7-2) и (7-4) определяют свойство симметрии, заключающееся в том, что средняя неопределенность того, какой символ будет получен, снимаемая при посылке конкретного символа, равна средней неопределенности того, какой символ был отправлен, снимаемой при приеме символа. С помощью полученной формулы (7-2) нетрудно вывести выражение для H(х,y) через соответствующие вероятности

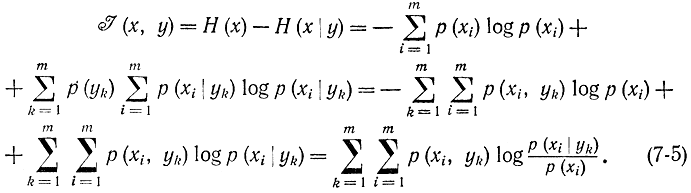
Аналогичным образом, используя формулу (7-4), получаем:

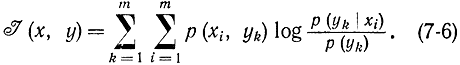
При этом следует учитывать, что

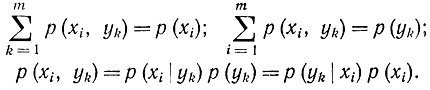
Оба выражения в правых частях (7-5) и (7-6) могут быть сведены к одной симметричной форме, если умножить дроби под знаком логарифма в формуле (7-5) на р(y_k), в формуле (7-6) на р(x_i) соответственно. В результате получим:

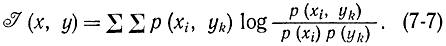
Аналогичным образом могут быть получены соотношения для непрерывных сигналов х и y:

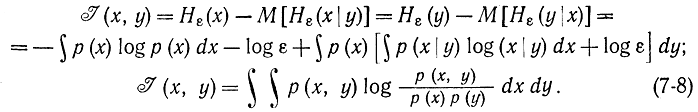
В большинстве теоретических работ используется формула (7-8) и при этом специально не оговариваются непрерывные или дискретные сигналы.

В частности, в формуле (7-8) величину I(х,y) можно интерпретировать, как относительную информацию объекта х относительно объекта y (или объекта у относительно объекта х), равную разности априорной и апостериорной энтропий объекта y (или х). Причем оба объекта могут быть или дискретными, или непрерывными (в последнем случае используются дифференциальные энтропии с одинаковым уровнем квантования ε). Один из объектов х может быть дискретен, а другой у непрерывен. В этом случае формула (7-8) определяет количество информации, равное разности априорной и апостериорной энтропий дискретного объекта х или разности априорной и апостериорной дифференциальных энтропий непрерывного объекта y

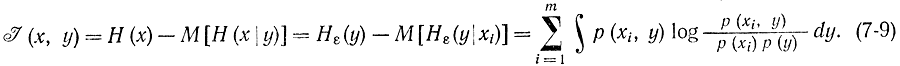
Симметрия является важным свойством информации, которое заключается в том, что I(x, y) одинаковым образом зависит от х и y и количество информации об объекте х, содержащееся в объекте Y, равно количеству информации об объекте y, содержащемуся в объекте х. Отсюда можно сформулировать четвертое определение количества информации: среднее количество информации есть мера соответствия двух случайных объектов, численное значение которой определяется формулой (7-8).