д) Критерий минимума критического времени выполнения работы

В последнее время в связи с интенсивным внедрением сетевых методов планирования и управления возникают задачи о критическом пути. Например, выполнение сложного проекта сводится к последовательности выполнения какого-то определенного количества работ. Для отображения этого процесса прибегают к геометрической интерпретации с помощью графа (рис. 10-6).

Узел графа обозначает конец одной работы и начало другой. Дуга или ребро графа - работа, а длина ребра пропорциональна времени выполнения работы. Пусть длительность выполнения отдельной работы t_ij=t_j-t_i, где t_i и t_j - моменты времени, соответствующие началу и концу работы. Критическим в графе будет такой путь, на котором суммарное время выполнения работ максимально. Этот путь задерживает всю разработку: без его уменьшения невозможно сократить время выполнения всей разработки. Критический путь определяется решением экстремальной задачи, в которой обращается в максимум следующее выражение:

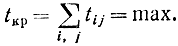
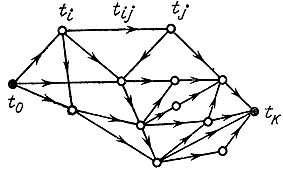
Рис. 10-6. Пример сетевого графика ведения комплексной работы

Суммирование в этой двойной сумме необходимо производить таким образом, чтобы получить путь из начальной вершины t₀ в конечную t_k без разрыва и дважды не пройти по одной и той же дуге. Критерий минимума критического времени

означает минимизацию критического пути при ограниченных ресурсах. При этом наличные ресурсы распределяются на те работы, которые лежат на критическом пути. В данном случае, по существу, решается минимаксная задача, характерная для теории игр:

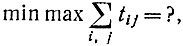
причем максимум выбирается среди всех путей в графе по времени выполнения работ, а минимум берется по ресурсам для работ, лежащих на критическом пути.