10-3. Классификация методов оптимизации

Классификация методов оптимизации представляет собой достаточно сложную задачу, так как в основном они исторически развивались независимо один от другого с использованием различных концепций, математических аппаратов и т. д. Однако инженеру- кибернетику необходимо знать их во всем многообразии.

Следует заметить, что приводимая классификация (как и любая классификация) носит условный характер и страдает недостатками. Поэтому относительно приводимых ниже схем можно высказывать замечания, но в целом они позволяют сразу охватить все особенности методов.

Возможно несколько подходов к классификации. Следует различать методы определения экстремума функции и функционала (рис. 10-7).

Хотя функция и является частным случаем функционала, методы отыскания экстремума функции проще. Методы динамического программирования и принципа максимума с успехом применяются для отыскания экстремума функционала и функции. Прямые методы вариационного исчисления (методы Ритца, Эйлера и др.), как и дискретный вариант уравнения Эйлера, сводят задачу отыскания Рис. 10-7. Общая структурная схема методов экстремума функционала к оптимизации, экстремуму функции. Методы

отыскания экстремума функции получили такое большое развитие в кибернетике в связи с вычислительными трудностями решения системы алгебраических уравнений вида

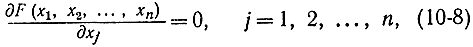
особенно при наличии ограничений на координаты x_j.

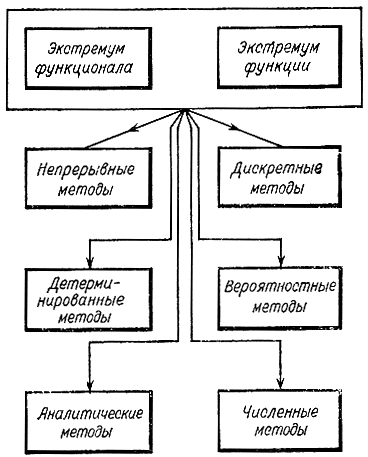
Рис. 10-7. Общая структура схема методов оптимизации

Классическая математика ограничивалась разработкой методов решения и доказательствами принципиальной разрешимости уравнений вида (10-8), что привело к созданию так называемых аналитических методов оптимизации. Однако при решении конкретных инженерных задач важно владеть процедурами, позволяющими доводить решение до числовых данных. Это заставило искать и разрабатывать численные методы оптимизации.

Спор между сторонниками аналитических и численных методов с позиций кибернетики в известном смысле потерял свою остроту, так как практика проектирования конкретных систем управления требует применения обоих методов. За аналитическими методами остается преимущество, заключающееся в возможности определения качественной картины поведения оптимальной системы при изменении ее параметров и структуры. Численные же методы обеспечивают получение конкретных числовых значений параметров управления. Некоторую, попытку рационального объединения этих методов можно усматривать в интенсивной разработке человеко-машинных методов оптимизации, использующих язык диалога человека и ЦВМ, большие банки данных и возможности современных операционных систем. При этом удается повторять вычисления при разных условиях, использовать, где необходимо, аналитические методы, представленные в виде стандартных программных блоков, и, самое главное, оперативно включать в процедуру отыскания оптимального управления интеллектуальные способности человека.

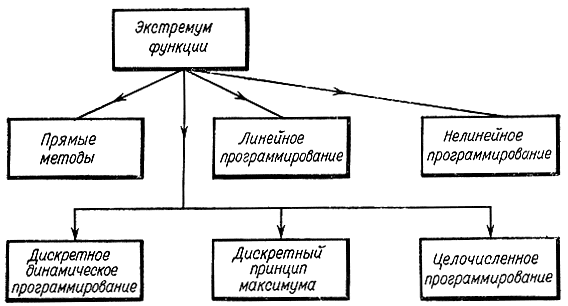
Рис. 10-8. Методы отыскания экстремума функции

Интересно отметить, что при таком способе оптимизации исходный критерий оптимальности может быть нестрого математически формализован в виде функции или функционала. Так, он может состоять из нескольких положений, сформулированных достаточно четко на словесном, содержательном уровне, что при наличии диалога человек - машина вполне допустимо.

Сложность решения уравнений (10-8) резко возрастает с увеличением числа переменных и ограничений на них. Поэтому большое развитие получили методы линейного и нелинейного программирования, прямые методы отыскания экстремума функции, а также дискретные принципы максимума и динамическое программирование (рис. 10-8).

Методы отыскания экстремума функционала ведут свое начало от классических методов Эйлера - Лагранжа - Гамильтона и заканчиваются динамическим программированием и принципом максимума (рис. 10-9). В них также содержатся прямые методы отыскания экстремума функционала и различные частные методы.

В соответствии со схемой на рис. 10-7 почти во всех методах (Эйлера - Лагранжа - Гамильтона, принципе максимума, динамическом программировании, прямых методах отыскания экстремума функции) можно выделить дискретные и непрерывные модификации, детерминированные и случайные варианты.

Дискретная задача оптимизации возникает всякий раз, когда требуется найти оптимальное значение переменных, которые заданы, так же как и функция от них, в виде набора дискретных значений.

В последнее время в связи с разработкой и внедрением АСУ чрезвычайно большое значение приобрели методы целочисленного программирования. Заметим, что одна из основных задач АСУ - оперативно- календарное планирование - относится к задачам целочисленного программирования. Единого общего метода решения задач целочисленного программирования нет. Разработано много способов решения пригодных для частного класса задач, среди которых большое место занимают нестрогие эвристические методы. Особого внимания среди них заслуживают лингвистические методы оптимизации. Они ближе всего подходят к человеческому способу мышления и удобны для реализации на ЦВМ с помощью проблемно-ориентированных языков. Здесь уместно снова упомянуть о человеко-машинных методах решения целочисленных задач оптимизации, являющихся по существу своему лингвистическими в широком смысле, так как они имитируют применяемые человеком методы оптимизации и планирования с добавлением эффективных аналитических и числовых процедур.

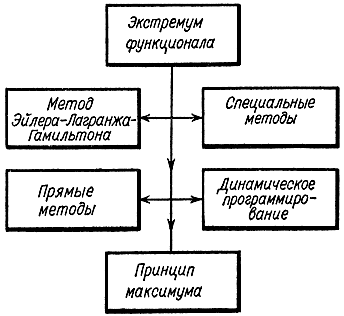
Рис. 10-9. Методы отыскания экстремума функционала

В заключение надо отметить, что в данном пособии одни и те же методы с разных точек зрения рассматриваются в разных разделах. Так, градиентный метод излагается в прямых методах отыскания экстремума функции и методах нелинейного (квадратичного и выпуклого) программирования. Во втором случае он используется как аналитический, в первом - как численный метод.

Замечание может вызвать имеющееся в пособии смешение двух принципов рассмотрения методов: по задачам и методу (или процедуре) решения. Динамическое программирование, принцип максимума и метод Эйлера - Лагранжа (в ограниченном плане) являются реализациями процедурного подхода. Первые два метода принципиально применимы ко всем задачам. По задачные методы представлены симплекс-методом для линейного программирования, различными процедурами решения задач нелинейного и целочисленного программирования.

Хотя с академической точки зрения такое разнообразие подходов может вызвать большие нарекания, но с точки зрения инженера кибернетика, который должен иметь на вооружении весь комплекс методов, такое изложение нам кажется оправданным.