Глава одиннадцатая. Методы классического вариационного исчисления

Прежде чем начать изложение аппарата классического вариационного исчисления, следует остановиться на некоторых понятиях.

Определим класс функций, с которыми имеет Дело классическое вариационное исчисление. Это непрерывные, кусочно-непрерывные, гладкие и кусочно-гладкие функции. График непрерывной функции представляет собой плавную кривую без разрывов (рис. 11-1, а). Кусочнонепрерывные функции имеют конечное число разрывов, которые по величине могут быть бесконечными и конечными (рис. 11-1,6): если при подходе к точке разрыва значение функции устремляется к бесконечности - это бесконечный разрыв (точка с), если у функции в точке разрыва существуют пределы слева и справа и разность между пределами конечная, то разрыв непрерывности называется конечным или разрывом первого рода (точка d). Разрыв считается устранимым, если пределы слева и справа в точке разрыва равны между собой, но значение функции в этой точке отлично от них. Решения вариационных задач иногда находят в классе гладких функций, у которых в заданном интервале непрерывна первая производная (участок cb на рис. 11-1, б), или кусочногладких, имеющих конечное число точек разрыва первого рода первой производной (рис. 11-1, г).

Классические методы вариационного исчисления не применимы к отысканию функций, оптимальных в классе функций, графики которых изображаются в виде, представленном на рис. 11-1, в. Для таких функций характерно наличие вертикальных участков, где первая производная принимает бесконечные значения. Однако такой вид оптимального управления наиболее интересен с практической точки зрения, в частности для задач максимального быстродействия. Это привело к необходимости разработки новых методов оптимизации типа методов Веллмана - Понтрягина- Кротова [Л. 69-75].

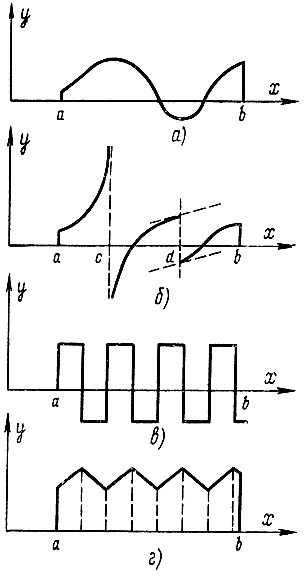
Рис. 11-1. Графики различных функций управления

Теперь рассмотрим понятия глобального и локального экстремумов. Глобальный экстремум достигается сравнением всех кривых данного класса, а локальный - сравнением только близких кривых. Например, требуется проложить кратчайшую дорогу между двумя пунктами, разделенными горой. Естественно, что ее следует искать среди путей, огибающих гору слева или справа. Допустим, наикратчайший путь слева короче, чем справа. Тогда путь слева будет давать глобальный экстремум, а путь справа - локальный.

Всякий глобальный экстремум одновременно и локальный, так как при определении глобального экстремума сравниваются все кривые данного класса, а при вокальном - только соседние.

Классическое вариационное исчисление основано на методе вариаций и дифференциальном уравнении Эйлера, вывод которого будет дан ниже. Это уравнение в различных модификациях встречается практически во всех методах вариационного исчисления, и поэтому ему уделяется особое внимание.