11-1. Уравнение Эйлера

Допустим, что на некоторой гладкой кривой, проходящей через точки a и b достигается экстремум функционала

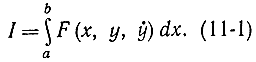
Определим необходимые условия, которым должна удовлетворять функция y(х), чтобы на ней достигался минимум. Сравним значения функционалов для близких к y(х) функций. Для этого придадим y(x) вариацию

где β - число; η(х) - произвольная гладкая функция, удовлетворяющая условиям η(а)=η(b)=0 и η(x)≥0.

Рассмотрим разность функционалов

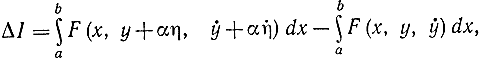
которая зависит от α. Разложим это приращение в ряд Маклорена по α (производные берутся при α= 0):

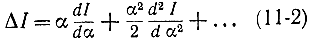
Выражение

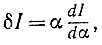
являющееся главной линейной частью функционала, называется первой вариацией функционала.

Аналогично

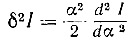
называют второй вариацией функционала. При малых α всеми членами в выражении (11-2), кроме первого, можно пренебречь, т. е.

Минимум на кривой y(x) достигается при условии

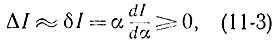
которое должно выполняться при любых а, положительных или отрицательных, если dI/dα=0. Это же условие справедливо и для максимума, только тогда в соотношении (11-3) перед нулем запишем знак "≤".

Для получения уравнения Эйлера используем формулы (11-1) и (11-2):

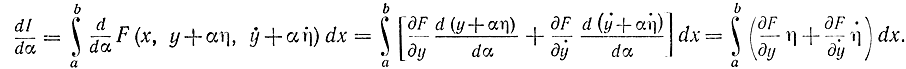
Проинтегрируем второй член по частям

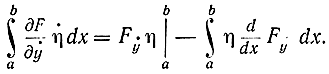
Так как η(x) обращается в нуль в точках a и b, то

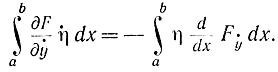
В результате

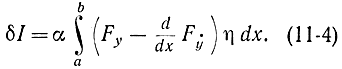
Теперь к выражению (11-4) требуется применить лемму Лагранжа, которая формулируется следующим образом: если непрерывная функция М(х) обладает тем свойством, что

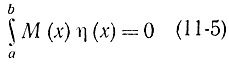
для любой гладкой функции η(x), то обязательно

для всех a≤x≤b.

Действительно, предположим противное: пусть хотя бы в одной точке c, где a≤c≤b, М(c)<0. Тогда выберем в качестве произвольной функции η(х) такую, которая больше нуля в окрестностях точки с, а на остальном интервале равна нулю (рис. 11-2). При таком выборе произведение М(х)η(х) в окрестности точки х=с и интеграл будут отличны от нуля, что противоречит исходному условию. Тем самым лемма Лагранжа доказана. Поэтому в соответствии с формулами (11-4) - (11-6) необходимое условие экстремума запишется как

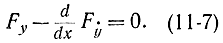
Это - знаменитое уравнение Эйлера. Общее решение его содержит две неопределенные постоянные, для определения которых требуется удовлетворение двух условий. Как правило, в качестве таких условий задаются значения функции y(x) в начале и конце интервала y(а) и y(b).

Таким образом, экстремальная задача сводится к решению нелинейного дифференциального уравнения с переменными параметрами, так как в общем случае функция F не-линейна относительно y и ẏ . Заметим, что

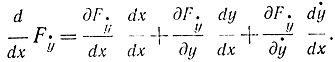
Подставляем это выражение в уравнение Эйлера и получаем:

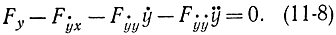
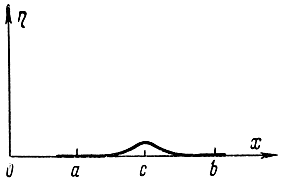
Рис. 11-2. Пояснение к теореме Лагранжа

Отсюда следует, ЧТО в общем случае Лагранжа, уравнение Эйлера является нелинейным дифференциальным уравнением второго порядка и поэтому его решить не удается.

При нашем выводе для справедливости этого уравнения требуется непрерывность как первой, так и второй производных функции y(х), т. е. заранее ставится условие непрерывности первых двух производных на экстремали. Это условие необходимо для применения леммы Лагранжа, так как она справедлива при непрерывности функции М(х), совпадающей с левой частью уравнения (11-8). Но требование непрерывности не дает возможности рассматривать очень важные для кибернетики функции управления в виде ступенчатых кривых с насыщением (рис. 11-1, в). Такая возможность появляется, как будет видно из дальнейшего, с применением принципа максимума Понтрягина, для которого характерно введение разрывных вариационных функций игольчатого вида. Заметим также, что вариация η(х) является гладкой функцией в классическом вариационном исчислении.

Пример 11-1. Рассмотрим задачу о длине кривой

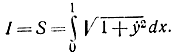
В данном случае

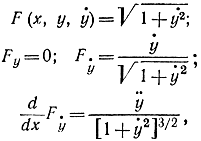
и уравнение Эйлера имеет вид:

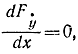
откуда дифференциальное уравнение для экстремалей и решение запишутся как

где C₁ и С₂ - постоянные интегрирования. Как и следовало ожидать, прямая линия обеспечивает кратчайшее расстояние между двумя точками.

Пример 11-2. Если в функционале (11-1) придать функции k(τ) вариацию αη(τ) и проделать необходимые преобразования, то условие dI/dα|_α=0 запишется [Л. 71] в виде интегрального уравнения Винера - Хопфа

Рассмотрим частные случаи уравнения Эйлера.

1. Пусть F не зависит от y. Тогда
   
   
   откуда
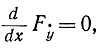   F_ẏ = const.
   Из последнего уравнения можно определить ẏ как функцию x и затем - искомую функцию y(x) как интеграл от этого решения.
2. Пусть F не зависит явно от x, т. е.
   F=F(y,ẏ )
   Тогда уравнение (11-8) запишется в следующем виде:
   
   
   Умножив все члены на ẏ, получим выражение
   
   
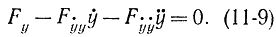   откуда
   
   
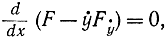   Уравнение (11-10) принято называть первым интегралом Эйлера. Умножать на ẏ уравнение (11-9) можно только при условии, что y не обращается в нуль. Следовательно, умножая на ẏ , можно потерять следующие решения вариационной задачи: ẏ =0, y=А, где А - корень уравнения F_y(A,0)=0.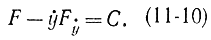
3. Допустим, что F зависит только от ẏ . В этом случае уравнение Эйлера принимает вид:
   
   
   следовательно, ẏ=const=k, и уравнение экстремалей запишется как
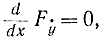   y=kx+b,
   т. е. экстремали будут прямыми линиями.
4. Наконец, допустим, что F_{ẏ ẏ} =0. В частности, это может быть, когда F=F(x, y) или F=М(х, y)+N(х,y)ẏ , т. е. функционал или совсем не зависит от производной ẏ , или зависит от нее линейно. Функционалы, для которых F_{ẏ ẏ} = 0, называются вырожденными в силу следующих соображений. Перепишем формулу (11-8)
   
   
   Из (11-11) видно, что для вырожденных функционалов не существует второй производной для экстремали, она не является кусочно-гладкой и, следовательно, допустимой функцией, для которой выводилось уравнение Эйлера.

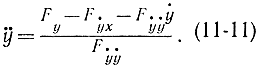
Для невырожденных функционалов F_{ẏ ẏ} может обращаться в нуль только в отдельных точках, за исключением которых формула (11-11) дает значение второй производной, т. е. экстремаль невырожденного функционала является кусочно-гладкой функцией, имеющей на отдельных участках непрерывную вторую производную. Изломы кривой могут быть в тех точках, в которых или F_{ẏ ẏ} =0, или числитель правой части формулы (11-11) терпит разрыв.

Эйлер получал уравнение другим методом, заменяя функционал

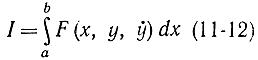
приближенно суммой вида

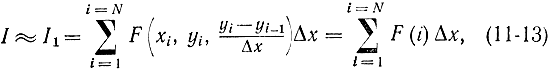
где

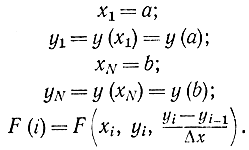
Благодаря такой замене вариационная задача о минимуме функционала (11-12) сводится к задаче о минимуме функции. Необходимым условием минимума функции является равенство нулю частных производных:

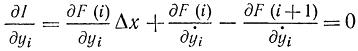
или

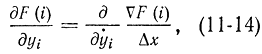
где ∇F(i)=F(i+1)-F(i).

Устремление Ал: к нулю в пределе переводит дифференциально разностное уравнение (11-14) в дифференциальное уравнение Эйлера (11-7).

Меняя местами операции дифференцирования и взятия разности в уравнении (11-14) и опуская индекс i, получаем:

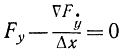
или

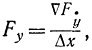
где

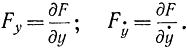
Это - дифференциально-разностное уравнение, определяющее значения y_i которые обращают в минимум сумму (11-13).

Величины x_i определяют разбиение на дискретные значения. В частности, можно считать, что Δх=1. Тогда

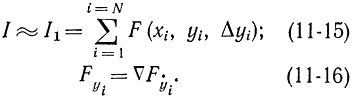
На эти уравнения можно посмотреть с другой точки зрения, считая, что требуется определить значения y_i (при заданных x_i), обращающие в минимум сумму (11-15), в которой, в частности, может быть одно слагаемое (N-1). Эта задача сводится к дифференциальноразностному уравнению (11-16). Можно еще упростить выражение (11-15), исключив переменные x_i. Для этого следует принять x_i=1,2,3..., что, по существу, уже было сделано, когда положили Δx=1 (теперь только изменено начало отсчета, т. е. x₁=1). Благодаря такому приему практически исчезла зависимость от переменных x_i и соотношения (11-15) и (11-16) можно переписать в виде

где

Эти соотношения могут служить основой при получении уравнений для дискретного динамического программирования и дискретного принципа максимума (см. гл. 12-14).

Однако в принципе максимума Понтрягина (и аналогичных соотношениях динамического программирования Беллмана) вместо функционала (11-12) рассматривается функционал вида

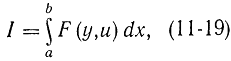
где y - координаты системы; u - управляющие координаты.

Формально функционал (11-19) получается из (11-12) заменой ẏ →u, а его дискретный аналог - из соотношения (11-17):

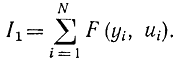
Получение уравнений, аналогичных (11-18), для случая такого задания оптимизируемой функции при определенных ограничениях на координаты y_i и составляет предмет дискретного принципа максимума (см. гл. 14). Заметим, что в выражении (11-17) зависимость от Δy_i носит весьма условный характер, так как величина Δy_i может быть заменена через y_i и y_i-1 в соответствии с формулой