11-2. Условие Лежандра

Помимо уравнения Эйлера можно было бы остановиться еще по крайней мере на трех необходимых условиях экстремума: Лежандра, Вейерштрасса и Якоби. Здесь будет рассмотрено только условие Лежандра, которое, помимо прочего, позволяет отличать минимум от максимума. Так как на экстремали первая вариация δI обращается в нуль, то знак приращения определяется в основном второй вариацией, поэтому в случае минимума δ²I≥0, в случае максимума δ²I≤0. Очевидно, что

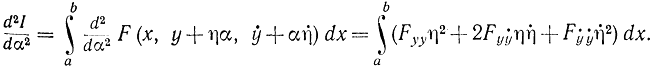
Преобразуем второй член этого выражения, взяв интеграл по частям:

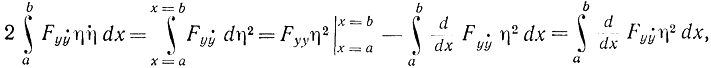
откуда

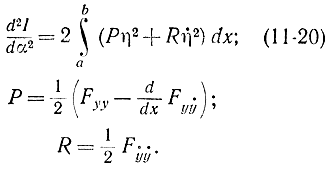
Из формулы (11-20) следует, что для выполнения условия минимума

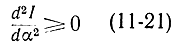
необходимо, чтобы

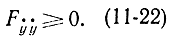
Действительно, поскольку функция η(x) произвольная, то ее всегда можно подобрать так, чтобы функция η² была мала, а η² велика. Выбор следует остановить на функции η(x), малой по абсолютной величине, но быстро и резко изменяющейся. У такой функции знак второй вариации совпадает со знаком F_{ẏ ẏ} . Напоминаем, что речь идет об определении необходимого условия минимума, т. е. если есть минимум, то это условие выполняется для любых η. Покажем, что для выбранной таким образом функции из формулы (11-21) следует (11-22). Для этого предположим обратное, т. е. что

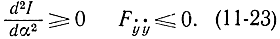
При таком выборе функция η получается малой, а ее производная - большой. Знак интеграла (11-20) определяется знаком R, т. е, знаком функции F_{ẏ ẏ} , а следовательно, соотношения (11-23) противоречивы и из выражения (11-21) следует (11-22). Тем самым условие Лежандра доказано.

Аналогичным образом можно показать, что для максимума