11-3. Задача с подвижными концами

Могут встречаться задачи более сложные, в частности такие, в которых концы кривых не закреплены: задачи с незакрепленными или подвижными концами. В этом случае вариация функционала зависит от вариации искомой функции и ее концов. На рис. 11-3 изображены исходная y(х) и проварьированная y(х)+h(х) функции.

Приращение функционала представим в форме

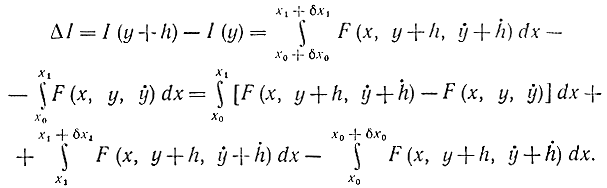
Здесь первый интеграл — вариация кривой, а два последних — вариации концов. Выделим главную линейную часть приращения — вариацию δI, для чего положим малыми h, ḣ , δx₀,δx₁:

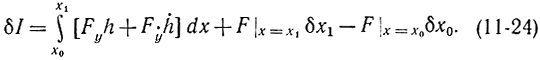
Второй член подынтегрального выражения в формуле (11-24) проинтегрируем по частям, в результате чего получим:

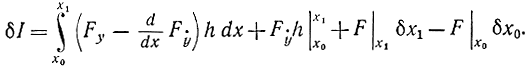
С точностью до бесконечно малых высшего порядка можно написать (см. рис. 11-3):

и тогда окончательно получим:

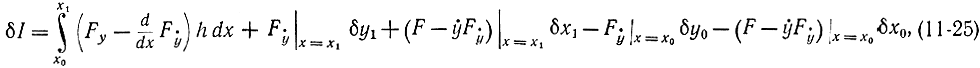
где есть интегральный член, зависящий от вариации кривой внутри первоначального интервала, и члены без интеграла, зависящие от вариации концов. Ниже с помощью этого соотношения получим ряд важных формул.

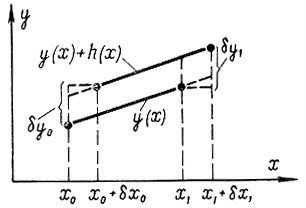
Рис. 11-3. Пояснения к вариационной задаче с подвижными концами