11-4. Условие трансверсальности

Часто требуется определить экстремум функционала среди кривых y(х), концы которых могут перемещаться по двум кривым

В общем случае в качестве границ могут выступать трехмерные и n-мерные кривые и поверхности в задачах, связанных с морскими переходами с одного материка на другой или космическими полетами между близко расположенными небесными телами. Примером такой задачи может быть определение минимального расстояния между окружностями (рис. 11-4). Для решения необходимо определить не только кривую, но и положение ее концов А и В, которые могут быть найдены из условия трансверсальности. Очевидно, что эта кривая должна быть экстремалью, так как в противном случае через те же точки А и В можно было бы провести другую кривую, дающую минимум расстояния, поэтому первый член в формуле (11-25) обращается в нуль и

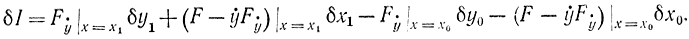
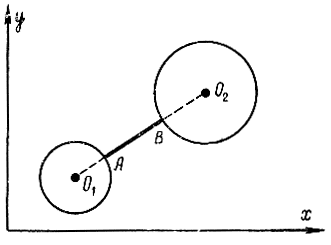
Рис. 11-4. Пояснение к задаче определения минимального расстояния между окружностями

С точностью до бесконечно малых высшего порядка запишем:

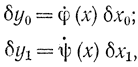
откуда условие экстремума δI=0 приобретет вид:

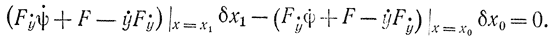
Так как δx₀ и - независимые друг от друга приращения, то

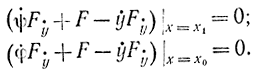
Эти соотношения называются условиями трансверсальности. Входящие в решение уравнения Эйлера две неопределенные константы могут быть определены из этих условий. Положения концов экстремали (точки x₀ и x₁) могут быть найдены как точки пересечения экстремали с кривыми: y=φ - первый конец; y=ψ - второй конец.

Условию трансверсальности можно дать интересную геометрическую интерпретацию, если рассмотреть функционал вида

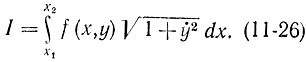
В этом случае

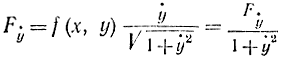
и условие трансверсальности запишется как

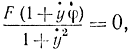
откуда следует, что

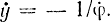
Аналогично для второго конца

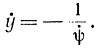
Но условия (11-27) и (11-28) означают, что кривая y(х) пересекает кривые φ(x) и ψ(x) под прямым углом, поэтому для функционалов вида (11-26) условие трансверсальности совпадает с условием ортогональности. К такого рода функционалам относится функционал, который определяет расстояние

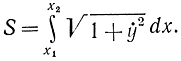
Отсюда можно утверждать, что кратчайшее расстояние между двумя кривыми получается вдоль третьей, им перпендикулярной. Так, для двух окружностей это будет перпендикуляр, проходящий через их центры.

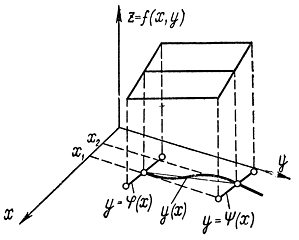
Рис. 11-5. Пояснение к функционалу (11-26)

Функционалу (11-26) также можно дать геометрическую интерпретацию (рис. 11-5). Функция z=f(х,y) определяет поверхность в трехмерном пространстве и физически может означать, например, расход топлива на единицу длины. Таким образом, интеграл означает полный расход топлива вдоль траектории, соединяющей две граничные кривые. Вариационная задача на минимум означает определение такой траектории y(х), соединяющей кривые y=φ(х) и y=ψ(х), вдоль которой расход топлива был бы минимален. Если рассмотреть интеграл вида

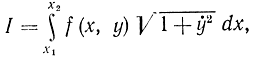
то его можно интерпретировать, в частности, с помощью поверхности вращения, которую описывает в трехмерном пространстве кривая, проведенная в плоскости (х, у) между кривыми y=φ(х) и y=ψ(х), при вращении вокруг оси Ох. В этом случае f(х,y) означает вес единичной площади. Элемент площади равен 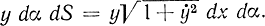. Физически минимум функционала

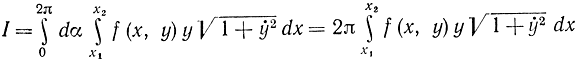
означает определение такой кривой y(х), для которой вес площади поверхности вращения минимален.