11-5. Задача на условный экстремума

Как уже упоминалось, в практике встречаются задачи на отыскание экстремума функционала при дополнительных условиях, наложенных на функции, в классе которых ищется экстремум. Это и есть задачи на условный экстремум. Их примером может служить задача о нахождении кратчайшего расстояния между двумя точками при условии, что кривая, соединяющая эти две точки, лежит на некоторой поверхности, например на сфере. Решение сводится к определению минимума функционала

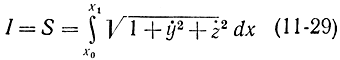
при условии

Прежде всего напрашивается мысль о том, чтобы выразить z через x, y из уравнения (11-30) и, подставив его в соотношение (11-29), решить обычную задачу на экстремум при одной переменной. Однако ограничивающие условия (11-30) могут быть очень сложными, и поэтому предпочитают другой путь - метод неопределенных множителей Лагранжа. Существует следующая теорема: для того чтобы найти экстремум функционала

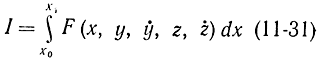
при условии

необходимо ввести вспомогательную функцию

где λ(х) - пока неизвестная функция (неопределенный множитель Лагранжа), и искать обычными методами экстремум функционала

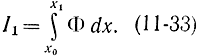
Таким образом, в задаче требуется определить три неизвестные функции y(х), z(х), λ(х), удовлетворяющие трем уравнениям: двум уравнениям Эйлера для функционала (11-33)

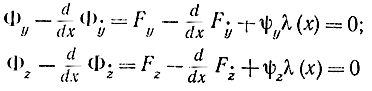
и одному уравнению связи

Докажем справедливость этой теоремы. Если исключить из рассмотрения особые случаи, то можно считать, что принципиально уравнение (11-32) разрешимо относительно z:

Подставив это выражение в функционал (11-31), получим:

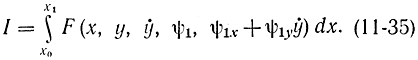
Если исходная задача имеет решение в виде пространственной кривой, которая обращает функционал (11-31) в минимум, то проекция этой кривой на плоскость (х, y) будет обращать в минимум функционал (11-35). Обозначив через F функцию аргументов х, y, ẏ , которая получается из функции F (х, y, ẏ,z, ż) заменой z=ψ₁(х, y), можем написать:

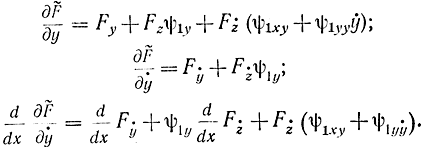
Учитывая эти соотношения, уравнения Эйлера для функции F

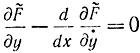
можно переписать в виде

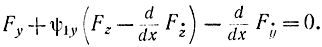
Дифференцируя условие (11-32) по y, получаем:

После исключения из этих двух последних уравнений получаем искомые соотношения:

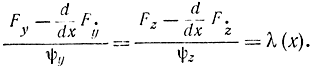
Тем самым теорема доказана, и доказан метод неопределенных множителей Лагранжа для задачи на отыскание условного экстремума. Это правило остается справедливым и для случая с несколькими ограничивающими условиями типа (11-32). При этом ищут экстремум функции

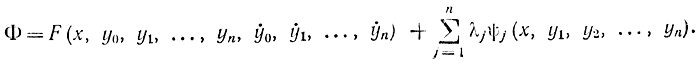
Наконец, правило неопределенных множителей Лагранжа сохра няется и тогда, когда ограничивающее условие содержит производит ψ(x, y, ẏ, z, ż). В этом случае экстремальная задача называется обобщенной задачей Лагранжа.

Для задачи на условный экстремум можно записать условие трансверсальности, при этом роль функции F будет играть функция Φ=F+λφ.

Примером задачи на условный экстремум является изопериметрическая задача, которая получила такое название из-за частной задачи определения среди всех кривых равной длины (изопериметрических) одной кривой, ограничивающей максимальную площадь. Здесь экстремум функционала

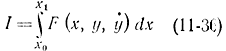
определяется при ограничивающем условии в виде интеграла

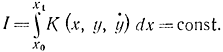
Данная задача сводится к обобщенной задаче Лагранжа введением функции Φ=F+λ₀Κ, после чего решается задача на глобальный экстремум функционала

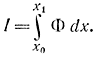
Интересно обратить внимание на принцип взаимности в изопериметрической задаче. Уравнение экстремалей не изменится, если в этом функционале Φ умножить на постоянное число. Тогда функция Φ запишется в виде

что означает возможность отыскания экстремума функционала I при постоянстве 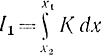и, наоборот, экстремума функционала I при постоянстве I - экстремали будут одни и те же. При этом не исключается случай с λ₀₁=λ₀₂=0.