11-6. Обобщенная задача Лагранжа. Задачи Майера и Больца

К обобщенной задаче Лагранжа сводятся почти все частные задачи вариационного исчисления. Так, при зависимости функционала от высших производных задача также решается методом Лагранжа. Действительно, если имеется функционал

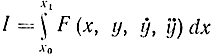
и введена новая функция ẏ=z, ÿ=ż , то решение сведется к отысканию экстремума функционала

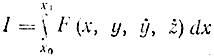
при условии

Задача Майера формулируется следующим образом. На промежутке [a,b] задана система m дифференциальных или алгебраических уравнений с n неизвестными функциями y_j(х):

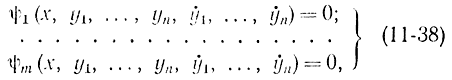
причем n<m. Если n=m, то уравнения (11-38) с граничными условиями полностью определяют функции y_j(х) и никакой вариационной задачи нет. При n>m имеется свобода варьирования и можно ставить задачу об отыскании n-m функций y_j(x), которые на одном из концов интервала [a, b] достигали бы экстремального значения. Примером может служить задача о разгоне двигателя, который должен достичь в момент Т максимальной скорости вращения ωТ.

Задачу Майера легко преобразовать к задаче Лагранжа, если ввести n=m новых переменных

Тогда она будет заключаться в нахождении экстремума функционала

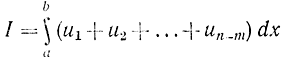
при ограничивающих условиях (11-38). Так, в задаче с двигателем этот функционал запишется как

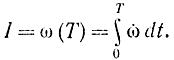
Можно и наоборот задачу Лагранжа свести к задаче Майера, поэтому правомерно считать их эквивалентными.

Задачей Больца или смешанной называется задача отыскания экстремума функционалов вида

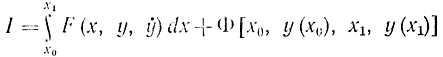
при наличии ограничивающих условий или уравнений связи. Эта задача эквивалентна задаче Лагранжа и сводится к ней, если ввести переменную

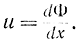
В этом случае функционал принимает вид:

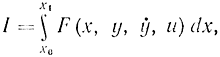
где

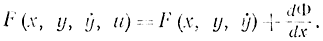
Можно Сказать, что все три задачи обладают одинаковой степенью общности.

Задача Майера (и задача Больца при F=0) интересна с той точки зрения, что формально в ней ищется функция, доставляющая экстремум функции, а не функционалу, заданному в виде интеграла, и тем самым как бы перекидывается мост между методами отыскания экстремума функционала и функции.