11-7. Задача с ограничениями в классическом вариационном исчислении
Уже указывалось, что на практике для достижения оптимального управления часто приходится отыскивать экстремум функционала при ограничениях, наложенных на класс сравниваемых функций ГЛ. 70. Дело в том, что например, мощности исполнительных устройств систем управления, как правило, ограничены (например, мощность электромеханических или гидравлических двигателей). Математически это означает, что для сравнения допускаются функции yj, удовлетворяющие неравенству
ψi(x, yj, ẏj)≤0, i=1,2,...,m
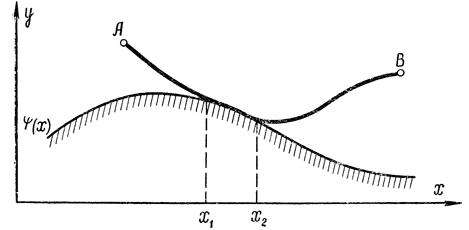
Рис. 11-6. Пояснение к задаче с ограничениями
Такие задачи удается решать на уровне инженерной строгости введением односторонних вариаций и дополнительным усложнением функционалов. При этом задача, естественно, усложняется. Начнем с простейшего случая, когда заданы функционал вида
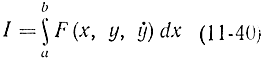
и ограничивающее условие
y(х)≥ψ(х). (11-41)
Кривая y=ψ(х) определяет границу области, внутри или вне которой должна находиться функция, доставляющая экстремум функционалу (рис. 11-6). Области, в которые включается граница, называются замкнутыми. Основная трудность в решении таких задач состоит в следующем. Для замкнутой области кривую y(х) можно
сравнивать только с кривой y+δy, так как если y(х) проходит по границе [y=ψ(x)], то кривая y-δy (δy>0) уже выходит за пределы допустимой области, т. е. на границе допустима только односторонняя вариация. При выводе же основного уравнения Эйлера использовались вариации обоих знаков y+δy и y-δy (δy>0) и значения функционала на экстремали y(х) сравнивались с его значениями для обеих допустимых функций y+δy и y-δy. Для того чтобы устранить это несоответствие, заменяют переменные: вместо y вводят z, пользуясь уравнением
z2=y-ψ(x)
из которого следует, что
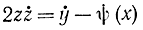
или
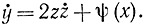
Поэтому функционал (11-40) в новых переменных может быть записан в виде
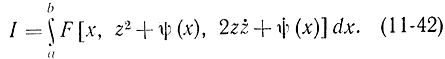
На новую функцию z(х) не наложено никаких ограничений, просто на границе области она принимает значение z=0, и экстремум функционала (11-42) можно искать обычным методом, придавая z двусторонние вариации. В результате получится уравнение Эйлера для функции z:
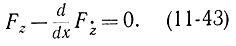
Но так как
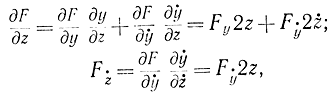
имеем:
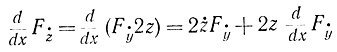
и уравнение Эйлера (11-43) может быть переписано:
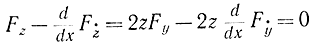
или
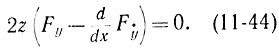
Уравнение (11-44) распадается на два: z=0, которое совпадает с уравнением y=ψ(x), и уравнение Эйлера
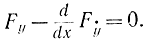
Из этих двух уравнений следует, что экстремум при наличии ограничений может достигаться лишь на кривых, составленных из кусков экстремалей и кусков границы допустимой области. В частных случаях длина одного из этих кусков может быть равна нулю.
Для полного решения задачи с ограничением необходимо найти условия перехода экстремали к границе области и наоборот. Допустим, что экстремум достигается на составной кривой и в точке * происходит переход от экстремали к границе области y=ψ(х) Для этого случая запишем:
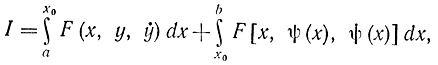
придадим точке перехода вариацию x0+δx0 и вычислим вариацию функционала, которая будет состоять из двух частей. Первая часть содержит вариацию на экстремали
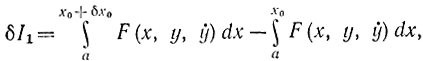
вторая - на граничной кривой
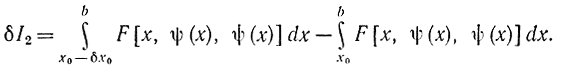
Вариация функционала на экстремали вычисляется по формуле вариации функционала со свободным правым концом, который перемещается по кривой y=ψ(x), т. е.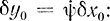
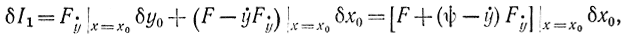
вариация функционала на граничной кривой
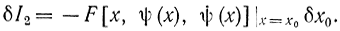
Так как экстремум должен удовлетворяться на составной кривой, то
δI1+δI2=0
Отсюда, учитывая произвольность δx0, получаем:
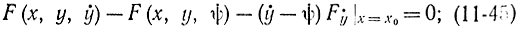
при этом учтено, что
ψ(x0)=y(x0)
Преобразуем разность F(x, y, ẏ )-F(х, y, ψ), используя теорему Лагранжа о среднем значении
f(a)-f(b)=(a-b)f(с), (11 -46)
где a≤c≤b, откуда
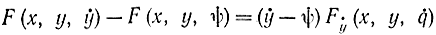
здесь q лежит между y и ψ. Формула (11-45) теперь запишется в виде соотношения
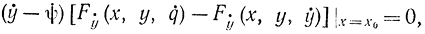
применив к которому снова формулу Лагранжа (11-46), получим:
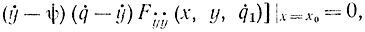
где q1 - промежуточное значение между q и ẏ (х0). Из этой формулы следует, что если Fẏ ẏ ≠ точке перехода х=х0, то ẏ=ψ, так как q=ẏ только при ẏ=ψ в силу того, что q - промежуточное значение между y и ψ. Таким образом, в точке сопряжения экстремали и граничной кривой касательные к ним должны совпадать. Это условие может не соблюдаться лишь при Fẏ ẏ =0, т. е. в отдельных особых точках функционала (в точках излома экстремали), или для вырожденных функционалов, для которых Fẏ ẏ =0.
Полученное условие непрерывности касательной дает дополнительное соотношение, необходимое для определения постоянных интегрирования. Если решается задача типа изображенной на рис. 11-6, то после нахождения уравнений экстремалей требуется определить шесть параметров: по две постоянные интегрирования для левого и правого участков экстремали и две для абсцисс точек перехода от одной экстремали к граничной кривой и от граничной кривой к другой экстремали. Эти константы находятся из шести уравнений, которые получаются (по два):
- из граничных условий прохождения экстремалей через точки А и В;
- из условия равенства ординат экстремалей ординатам граничной кривой к точкам сопряжения
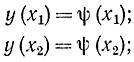
- из условия равенства производных на экстремалях производным на границе области в точках сопряжения
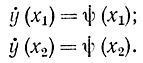
Теперь рассмотрим условие, которому должна удовлетворять кривая, обращающая функционал в экстремум на границе области. Пусть требуется найти функцию y(х), которая дает минимум функционалу (11-40) при ограничивающем условии (11-41). Придадим y(х) вариацию δy на границе, где y=ψ(х). Чтобы не выйти из области допустимых функций y(х), необходимо иметь δy>0. Вариацию функционала при переходе от кривой ψ(x) к кривой ψ(x)+δy можно представить в виде
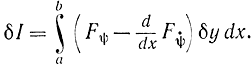
Чтобы функция y(x) доставляла минимум, необходимо иметь δy≥0, но здесь используется односторонняя вариация δy>0, поэтому из этого соотношения не следует, что
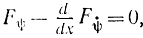
и можно лишь утверждать, что
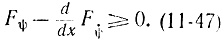
Отсюда видно, для того чтобы функция y(х) доставляла минимум функционалу (11-40) при условии (11-41), необходимо выполнение уравнения Эйлера для участков кривой, состоящей из экстремалей, и неравенства Эйлера (11-47) для участков, состоящих из граничных кривых. Из этого неравенства следует очень важное соотношение, которое может быть получено следующим образом. Проведем в некоторой точке 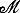 граничной кривой, доставляющей экстремум, экстремаль
граничной кривой, доставляющей экстремум, экстремаль 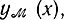 , касательную к границе области ψ(х), так что
, касательную к границе области ψ(х), так что
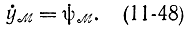
Так как на экстремали удовлетворяется равенство
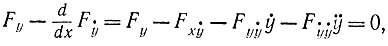
то, вычитая его из равенства (11-47) и учитывая (11-48), имеем:
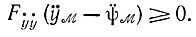
Отсюда при условии, что для минимума Fẏ ẏ ὅ0 и полагая Fẏ ẏ ≠0, получим искомое соотношение
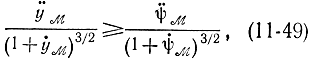
означающее, что кривизна экстремали не должна быть меньше кривизны граничной кривой в точке перехода с экстремали на граничную кривую: Ky≥Kψ Соответственно радиус кривизны экстремали не должен быть больше радиуса кривизны граничной кривой: Ry≥Rψ Для максимума знаки в этих соотношениях поменяются на обратные. Кроме того, условия y≥ψ и δy≥0 справедливы, когда экстремаль лежит над ограничивающей кривой. В противном случае все знаки при условии минимума меняются на противоположные:
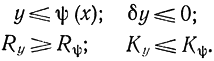
Это правило очень удобно применять для выяснения качественной, а иногда и точной геометрической конфигурации экстремалей и граничных кривых.
Пример 11-3. Найдем кратчайший сухопутный путь между точками А (1; 0,5) и В (3,5; 3), не заходящий на круглое озеро радиусом 1 и центром в точке O(2; 2) (рис. 11-7), Для этого определим минимум функционала
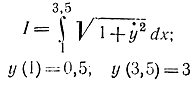
при наличии ограничении
(x-2)2+(y-2)2≥1
Экстремали приведенного интеграла - прямые линии. Экстремум достигается на составных кривых. Если
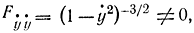
то в точках сопряжения касательные непрерывны. Искомый путь пройдет из точки А по касательной к окружности, далее по окружности и затем снова по касательной к ней, проходящей через точку В. Действительно, если рассматривать нижний участок АА1В1В, то для него ψ>0 и область допустимых экстремалей лежит под окружностью. Поэтому δy<0 и ψ>y. Так, переход с экстремальной кривой, представляющей собой прямую линию АА1 на нижнюю часть окружности разрешается, но только в точке касания прямой и окружности. Аналогично на участке АА2В2В ДЛЯ перехода на окружность необходимо, чтобы
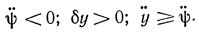
Переход на окружность разрешается также в точке касания A2. Переход с окружности на прямые В1В и В2В разрешается в точках касания В1 и В2. Задача имеет два решения: на нижней кривой АА1В1B достигается абсолютный экстремум, на верхней кривой АА2В2В - относительный.
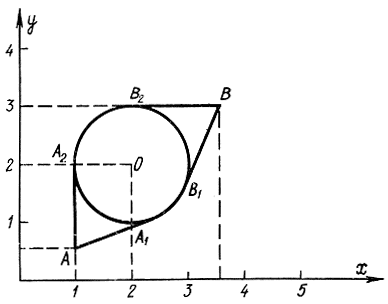
Рис. 11-7. Пояснение к примеру 11-3 (первый случай)
Для случая, когда озеро не круглое (рис. 11-8), с помощью формулы (11-49) можно графически построить путь, соединяющий точки А и F и не заходящий на озеро. От точки А до точки В движение происходит по прямой линии,представляющей собой экстремаль. В точке касания В этой прямой с кривой контура озера осуществляется переход на эту кривую, который разрешается при
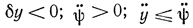
В точке С, для которой еще сохраняется условие ψ≥0 (не доходя до точки перегиба), осуществляется переход на прямую CD, имеющую с контуром озера касания в точках С и D. Движение по участку контура CC1D не разрешается, так как для него не выполняется требование ψ≥y, обусловленное тем, что δy<, так как ψ<, а ÿ=0.
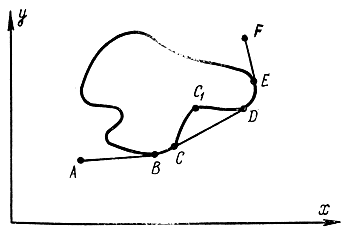
Рис. 11-8. Пояснение к примеру 11-3 (второй случай)
Ограничения могут быть более сложного вида, чем формула (11-41). В частности, ограничение может быть наложено на производную
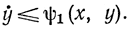
В этом случае неравенство заменяем равенством
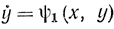
и, решив, его, получаем:
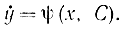
Переменные здесь целесообразно заменить в соответствии с формулой
z2=y-ψ(x,C)
Могут встретиться экстремумы, зависящие от нескольких функций:
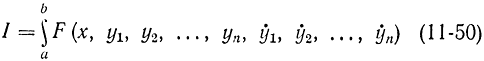
или
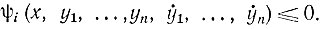
Допустим, что экстремум тогда достигается на кривой
y1(x),..., yn(x),
и, придавая поочередно вариации каждой из этих функций при неизменных остальных, получим тот же результат. Касательные в точке сопряжения равны, поэтому на границе области неравенство (11-51) перейдет в равенство, т. е.
ψ(x, y1,...,yn) (11-52)
а при зависимости функционала от одной функции
ψ(x,y)=0
откуда сразу найдется искомая функция y(х). Для функционала от n функций в уравнение границы входят я неизвестных функций, и чтобы определить участки границы, необходимо найти экстремум функционала (11-50) при связях (11-52).
Пример 11-4. Рассмотрим задачу, в которой решение имеет место только на границе. Определим минимум функционала
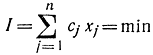
при ограничениях
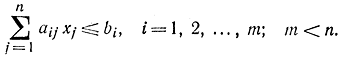
Сведем задачу к задаче Майера, вводя дополнительную переменную
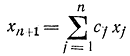
и считая, что ограничения имеют форму равенств:
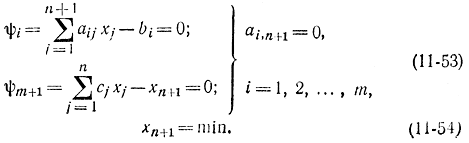
Ее можно свести к обобщенной задаче Лагранжа, считая дифференцируемыми функциями некоторой переменной t. Тогда, если ввести переменную un+1=xn+1, условие (11-54) сведется к минимуму функционала
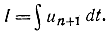
Функция Лагранжа определяется по формуле
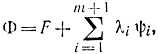
где ψi находится из (11-53), а функция
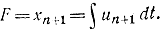
Очевидно, что здесь Φẋẋ=0 и имеет место особый случай с вырожденным функционалом.
Пример 11-5. Заданы не голономные, т. е. зависящие от производных, ограничения
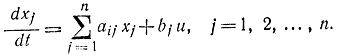
Определим координаты х системы и управляющее воздействие и таким образом, чтобы функционал
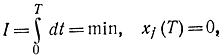
и при условии, что на u(t) наложено ограничение:
|u|≤1
Нетрудно видеть, что здесь тоже имеет место вырожденный случай, когда Φẋẋ=0 так как
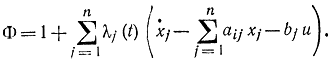
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'