11-8. Вырожденные функционалы
В классическом вариационном исчислении, как правило, не рассматривается случай вырожденного функционала Fẏ ẏ =0. Однако разработано много методов для частных случаев вырожденных функционалов. Потребностям инженера-математика наиболее отвечает метод Кротова [Л. 75].
Метод Кротова позволяет находить решения, геометрически изображаемые кривыми с вертикальными участками или, более строго, с участками бесконечных значений первой производной.
Из предыдущих рассуждений следует, что равенство нулю второй производной F может приводить к скачкам первой производной, в результате которых происходит излом экстремали. При конечном числе скачков решение можно получить, используя условия (11-25), которые в данном случае будут иметь вид условий Вейерштрасса-Эрдмана [Л. 70, 75]. Однако эти условия не позволяют определять решения, содержащие участки с бесконечными значениями первой производной.
Как уже указывалось, если Fẏ ẏ 0, то функционал можно представить в виде
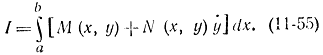
Уравнение Эйлера при этом запишется как
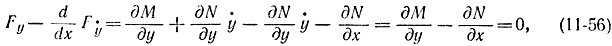
откуда видно, что оно является не дифференциальным, а алгебраическим или конечным уравнением, не содержащим производной от искомой функции. Отсюда могут иметь место два случая.
- Алгебраическое уравнение (11-56) удовлетворяется тождественно. Тогда, учитывая, что ẏdx=dy, напишем:
или
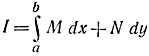 где
где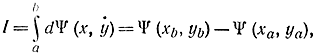 откуда в силу уравнения (11-56) имеем:
откуда в силу уравнения (11-56) имеем: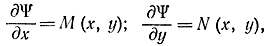 Таким образом, можно утверждать, что условие (11-56) является необходимым и достаточным (при непрерывности и дифференцируемости функций), для того чтобы подынтегральная функция была бы полным дифференциалом. В этом случае функционал не зависит от пути интегрирования, а зависит только от начальных и конечных точек. Для любой функции y(х) функционал сохраняет одно и то же значение. Поэтому в известной степени вариационная задача об экстремуме функционала теряет свой смысл. Пример 11-6. Найдем экстремум функционала
Таким образом, можно утверждать, что условие (11-56) является необходимым и достаточным (при непрерывности и дифференцируемости функций), для того чтобы подынтегральная функция была бы полным дифференциалом. В этом случае функционал не зависит от пути интегрирования, а зависит только от начальных и конечных точек. Для любой функции y(х) функционал сохраняет одно и то же значение. Поэтому в известной степени вариационная задача об экстремуме функционала теряет свой смысл. Пример 11-6. Найдем экстремум функционала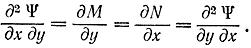 В этом случае уравнение Эйлера превращается в тождество 1 = 1 и функционал не зависит от пути интегрирования. Действительно,
В этом случае уравнение Эйлера превращается в тождество 1 = 1 и функционал не зависит от пути интегрирования. Действительно,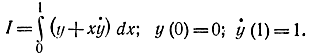 т. e. при любой кривой, соединяющей точки (0; 0), (1; 1), значение функционала будет одно и то же.
т. e. при любой кривой, соединяющей точки (0; 0), (1; 1), значение функционала будет одно и то же.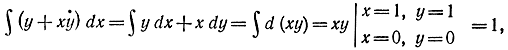
- Алгебраическое уравнение (11-56) выполняется не тождественно. Тогда оно определяет одну или несколько экстремальных кривых.
Метод Кротова отыскивает экстремали в классе кусочно-непрерывных кривых с вертикальными отрезками.
Пример 11-7. Найдем экстремаль, которая дает минимум функционалу
Здесь F ẏẏ = 2х2. Это выражение обращается в нуль при х=0, что означает наличие вертикальных участков экстремалей при х=0. Данный пример хорошо показывает, что равенство Fẏẏ=0 не исчерпывается функционалом вида (11-55). Уравнение Эйлера в данном случае имеет вид:
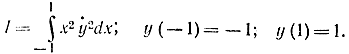 и его решением будут гиперболы
и его решением будут гиперболы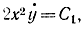 и его решением будут гиперболы однако ни одна из них не проходит через точки (-1, -1), (1; 1), а минимум функционала существует и равен нулю. Нулевое значение функционалу будет придавать функция, показанная на рис. 11-9:
и его решением будут гиперболы однако ни одна из них не проходит через точки (-1, -1), (1; 1), а минимум функционала существует и равен нулю. Нулевое значение функционалу будет придавать функция, показанная на рис. 11-9: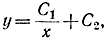
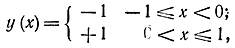 которая в точке х=0 терпит скачок.
которая в точке х=0 терпит скачок.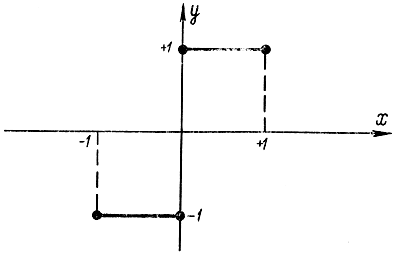
Рис. 11-9. Пояснение к примеру 11-7
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'