11-9. Каноническая форма уравнений Эйлера

При оптимизации можно пользоваться симметричной или канонической формой дифференциальных уравнений, ведущих свое начало из вариационной механики Гамильтона - Лагранжа.

Если ввести вместо ẏ новую переменную

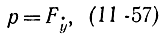
то можно считать, что для случая не особого функционала из нее можно выразить ẏ =φ(х, y, p). Поэтому если ввести функцию, называемую гамильтонианом

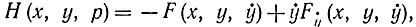
где ẏ=φ(p), т. е.

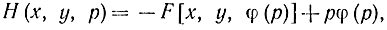
то прямым дифференцированием можно получить следующие уравнения:

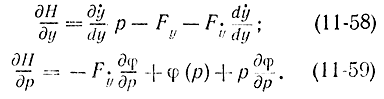
Заметим, подставив в уравнение Эйлера

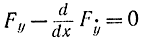
формулу (11-57), получим:

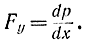
С учетом последнего соотношения и формулы (11-57) уравнения (11-58) и (11-59) примут вид:

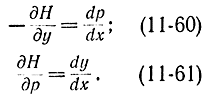
Это - гамильтонова форма уравнений Эйлера, представляющая собой связанную пару дифференциальных уравнений в частных производных. Иначе их называют канонической формой уравнений Эйлера или уравнениями Гамильтона - Эйлера.

Иногда вводят функцию Н₁=-Н, тогда из первого уравнения знак "минус" переходит во второе. Переменные p и y называются каноническими. С их применением условие Вейерштрасса - Эрдмана записывается в виде

Если имеется задача Лагранжа, то для вспомогательной функции

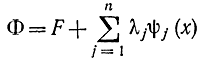
можно записать уравнение Эйлера

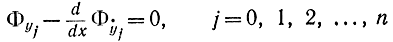
и уравнения Гамильтона - Эйлера

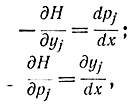
где

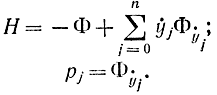
Если имеется обычная задача на экстремум для случая n переменных, то вместо n уравнений Эйлера

можно записать 2n уравнений Гамильтона - Эйлера

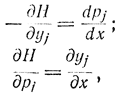
где гамильтониан

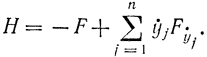
Функция Гамильтона H выбрана равной левой части первого интеграла Эйлера [формула (11-10)], так как во многих задачах это выражение сохраняет постоянное значение, если функция F или Φ явно не зависит от х. Такой независимости можно достичь специально путем выбора переменных и ограничивающих условий, как это делается в принципе максимума Понтрягина. Этот метод целиком заимствован из вариационной механики, где часто истинное движение происходит таким образом, что функция Гамильтона сохраняет постоянное значение.

Существует такое построение теоретической механики [Л. 76], в котором все основано на уравнениях движения Гамильтона и функции Гамильтона, которая принимается как

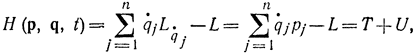
где t соответствует х; q (в простейшем случае) - обобщенная координата; р (в простейшем случае р=mv=mẏ ) - обобщенный импульс системы; L - функция Лагранжа, которая в простейших случаях равняется разности кинетической и потенциальной энергий

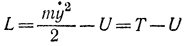
или

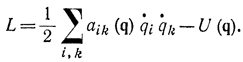
Состояние любой физической или механической системы характеризуется в определенный момент времени t координатами q и их производными q или импульсами Р, поэтому состояние системы в момент времени t может быть представлено точкой в фазовом пространстве 2n измерений, по осям координат которого отложены p_i и q_i. Вследствие этого функции L и Н зависят только от q и не содержат более высоких производных.

В простейшем случае функция Н равна сумме кинетической и потенциальной энергий системы. Действительно, величина 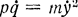равна удвоенной кинетической энергии, поэтому

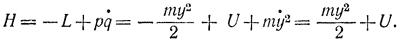
В механике есть принцип наименьшего действия или принцип Гамильтона, который формулируется следующим образом. Переход системы из одного состояния {q⁽¹⁾} в момент t₁ в другое состояние {q⁽²⁾} в момент t₂ происходит по такой траектории в фазовом пространстве, на которой интеграл действия обращается в минимум:

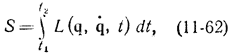
т. е. траектория движения системы в фазовом пространстве представляет собой экстремаль, которая дает минимум функционалу (11-62). Очевидно, что задача отыскания этой траектории может быть сведена к решению дифференциального уравнения Эйлера вида

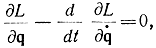
которое в механике носит название уравнения Лагранжа второго рода. Тем самым устанавливается связь теории вариационного исчисления и вариационной механики Лагранжа - Гамильтона.

При введении функции Гамильтона

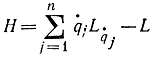
для получения уравнений движения Гамильтона, эквивалентных уравнениям Лагранжа второго рода, поступаем так же, как и в вариационном исчислении, т. е. вводим новую переменную - обобщенный импульс

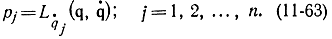
Считая, что эти уравнения можно разрешить в виде

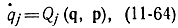
получаем выражение гамильтониана H через канонические переменные p_j и q_j.

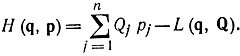
Дифференцируя это выражение аналогично уравнениям (11-58) и (11-59), с помощью равенств (11-39) получаем уравнения Гамильтона - Эйлера:

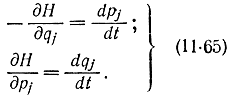
Важно отметить, что если рассматривать функции

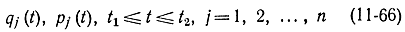
как произвольно и независимо заданные, в частности не связанные соотношением (11-64), то уравнения (11-65) будут двумя уравнениями Эйлера для функционала

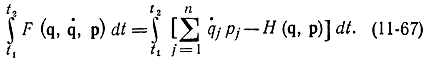
Действительно, если подставить выражение 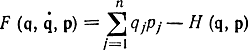в уравнение Эйлера

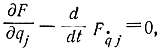
то получим второе уравнение (11-65), а если это же выражение подставить в

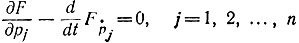
то получим первое уравнение (11-65). Поэтому принцип Гамильтона иначе формулируется следующим образом: траектории (11-65) в консервативном поле сил, для которого гамильтониан не зависит от времени, являются стационарными кривыми функционала (11-67), где Y(q, р) является соответствующим гамильтонианом, вдоль которых он сохраняет постоянное значение, так как является первым интегралом Эйлера. Термин "стационарный", а не "экстремальный" используется потому, что если р и q - независимые переменные, то интеграл (11-67) не имеет ни минимизирующих, ни максимизирующих кривых. Хотя данный вариационный принцип не является принципом максимума или минимума (если рассматривать р и q как независимые переменные), он может быть сформулирован как минимаксный принцип, что будет показано ниже.

Для наиболее распространенного случая

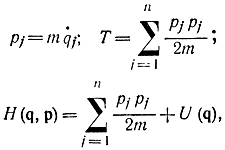
и канонические уравнения будут иметь вид:

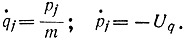
Пример 11-8. Проследим движение груза, закрепленного на двух пружинах (рис. 11-10). Кинетическая и потенциальная энергии груза равны:

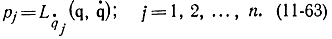
где m - масса груза; k/2 - жесткость каждой пружины. Введем обобщенную координату q и импульс р. Тогда выражения для кинетической и потенциальной энергий примут вид:

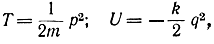
а функция Лагранжа

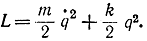
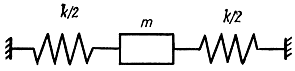
Рис. 11-10. Пояснение к задаче с пружиной

Соответствующее уравнение Эйлера запишется следующим образом:

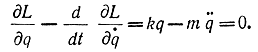
Это есть не что иное, как уравнение Ньютона

mẍ=kx,

которое отражает второй закон Ньютона из механики, утверждающий, что сила F=kx пропорциональна ускорению ẍ.

Таким образом, принцип минимума (максимума) находит широкое применение в теоретической механике. Понтрягин создал аналогичный формальный аппарат для систем управления - принцип максимума.

При решении задач оптимального управления специально вводят функцию Н таким образом, чтобы она явно не зависела от переменных t или х (как в случае принципа максимума Понтрягина). В этом случае существует первый интеграл задачи Эйлера - Лагранжа, который запишется в виде

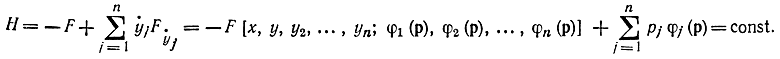
Далее показывается, что постоянное значение при оптимальном управлении имеет экстремальное (максимальное) значение.

Интересно отметить, что вариационная задача, которая формулируется в виде канонических уравнений Гамильтона - Эйлера, может быть сформулирована как минимаксная. Будем здесь использовать формализм вариационной механики, но очевидно, что полученные соотношения без труда могут быть записаны и для задач управления. При этом просто следует иметь в виду, что х↔t, y↔q, p↔p.

Будем считать p_j и q_j независимыми переменными и допустим, что рассматривается фиксированный путь:

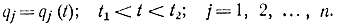
Исследуем интеграл

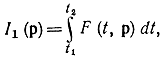
где

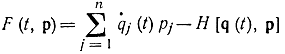
и

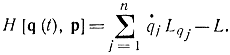
Нетрудно убедиться, что максимального значения этот интеграл достигнет в случае, если функции p_j(t), t₁<t<t₂ удовлетворяют условиям

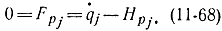
Действительно, уравнение (11-68) является уравнением Эйлера для подынтегральной функции 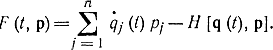- в этом нетрудно убедиться, если подставить это выражение в соответствующее уравнение Эйлера:

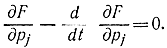
Существование максимума в данном случае обеспечивается тем, что функция F является полиномом второго порядка относительно переменных р, у которого члены второго порядка образуют отрицательно определенную квадратичную форму. Так, для n-1

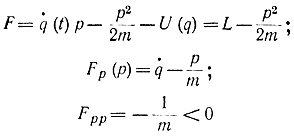
(это - максимум, потому что m>0). Так как уравнение (11-68) совпадает со вторым уравнением Гамильтона - Эйлера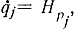
, которое эквивалентно

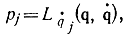
то условие максимизации интеграла (11-68) эквивалентно замене 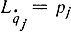в выражении для Н (q, р) или

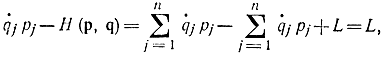
поэтому

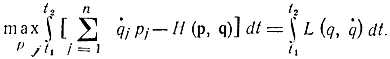
В соответствии с принципом наименьшего действия Гамильтона движение происходит так, что

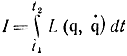
достигает минимального значения. Поэтому траектории движения q_j(t) и p_j(t) в консервативном поле сил являются решением минимаксной задачи:

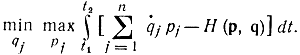
Физически минимаксный принцип означает, что движение должно происходить по таким траекториям и таким образом, чтобы максимум интеграла обеспечивался за счет кинетической, а минимум - за счет потенциальной энергии (или максимум за счет импульса р_j, а минимум за счет координаты q_j).

Только что изложенная минимаксная трактовка очень близка к принципу неопределенности в квантовой механике, когда нельзя одновременно со сколько- нибудь высокой точностью измерить координату и импульс частицы, и принципу неопределенности в теории информации, когда нельзя одновременно передавать (или формировать, получать) сигнал с какой бы то ни было узкой полосой по частоте и какой бы то ни было малой продолжительностью во времени.

Второе уравнение Гамильтона - Эйлера (11-61) в классическом изложении, т. е. с учетом связи (11-63) между р_j и q_j, не связано с уравнением Лагранжа - Эйлера и определяется формализмом обозначений.

Первое уравнение Гамильтона - Эйлера (11-60) определяется уравнением Лагранжа - Эйлера.

В только что рассмотренной неклассической процедуре, когда q_j и p_j - независимые переменные, второе уравнение (11-61) придает интегралу минимум, а первое уравнение (11-60) - максимум. Следует иметь в виду, что деление уравнений Гамильтона - Эйлера на первое и второе носит условный характер и в разных руководствах трактуется по-разному.

Минимаксная трактовка оптимального управления будет рассматриваться и дальше, особенно в нелинейном программировании в связи с фундаментальной теоремой Куна - Таккера (см. гл. 17).