11-10. Прямые методы вариационного исчисления

В большинстве практических задач уравнение Эйлера - Лагранжа не интегрируется. Поэтому большое распространение получили так называемые прямые методы, которые дают приближенное решение задачи [Л. 69, 77].

Идея прямых методов заключается в следующем. Пусть требуется найти функцию y(х), доставляющую экстремум функционалу I(y).

Построим последовательность функций y₁, y₂,...,y_n, которая сходится к функции y, т. е.

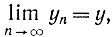
и докажем, что при этом функционал также стремится к некоторому пределу

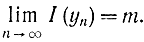
Существует много прямых методов. Из них наиболее известны методы Ритца и Эйлера, для которых с помощью достаточно сложных математических рассуждений доказывается, при каких условиях обеспечивается сходимость последовательности функций к экстремали.