а) Метод Ритца

Допустим, требуется найти минимум функционала

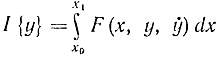
при граничных условиях

Введем в рассмотрение функции

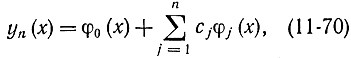
где

Функции φ_i - линейно-независимые и называются координатными, т. е. для них тождество c₀φ₀+c₁+φ₁+...+c_nφ_n=0 выполняется только при c_j=0, j=1,...,n. Если подставить выражение (11-70) в (11-69), то функционал превратится в функцию n переменных c₁, c₂,...,c_n т. е.

Требуется определить значения c_j, которые обращают в минимум функцию Q, т. е. задача сводится к решению n алгебраических уравнений:

Во многих случаях найденные таким образом функции y_n(x) сходятся к экстремали. В частности, условия сходимости выполняются для функционалов вида

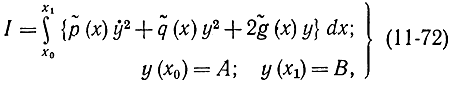
где 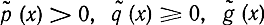- известные непрерывные функции. Для этого функционала уравнение Эйлера имеет вид:

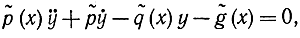
поэтому такие задачи называются линейными вариационными задачами.

Для функционалов типа (11-72) алгебраические уравнения (11-71) получаются линейными с определителем, отличным от нуля. В этом нетрудно убедиться, если в формулу (11-72) подставить (11-70):

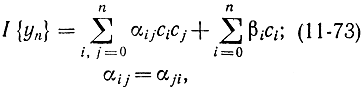
где α_i,j, β_i- некоторые постоянные, зависящие от конкретного вида функционала. После дифференцирования выражения (11-73) получим для определения коэффициентов с,- систему линейных алгебраических уравнений:

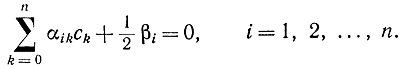
Пример 11-9. Минимизируем функционал [Л. 77]

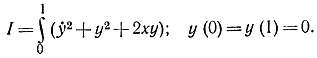
Для этого выберем координатные функции φ_i в виде

и при n=2 получим:

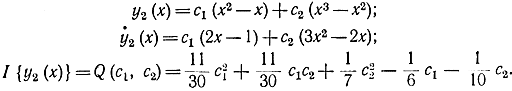
Тогда уравнения для определения значений коэффициентов c₁ и c₂ запишутся как

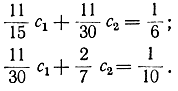
Отсюда

Точное решение в данном случае имеет вид:

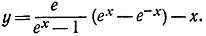
В табл. 11-1 дается сравнение точного и приближенного решений задачи.

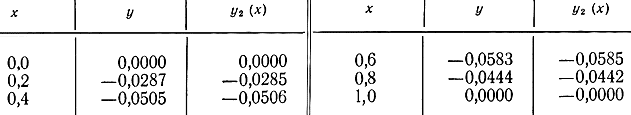
Таблица 11-1