б) Метод Эйлера (метод конечных разностей)
Согласно этому методу, который может рассматриваться как модификация метода Ритца, функционал
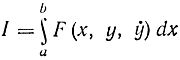
заменяется суммой по одной из приближенных формул численного интегрирования, которая зависит от значения yш в дискретных точках xi разбиения интервала изменения х (рис. 11-11).
Большинство формул численного интегрирования основано на замене подынтегральной функции полиномом, полученным из интерполяционной формулы Ньютона:
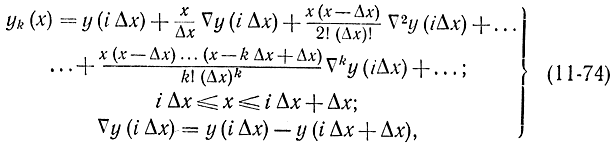
где Δx - интервал дискретности.
Рис. 11-11. Пояснение к методу Эйлера
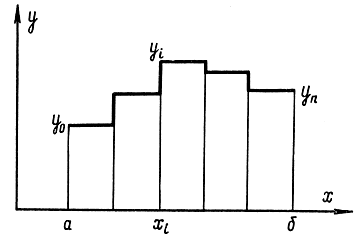
Рис. 11-12. Пояснение к методу Эйлера для случая аппроксимации прямоугольниками
В случае функционала I{х, y, ẏ} следует сделать замены
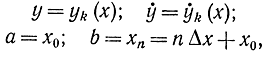
в результате которых функционал выразится суммой
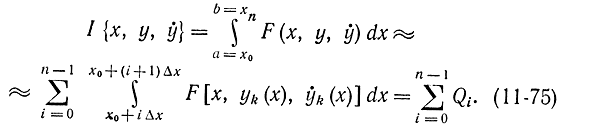
Подставив в это соотношение формулу (11-74) и выполнив интегрирование, получим функционал, зависящий только от значений yi:
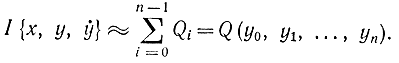
В результате задача сведется к решению системы алгебраических уравнений вида
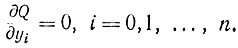
В зависимости от числа членов k в соотношении (11-74) получаются различные приближенные формулы. Так, если использовать аппроксимацию в виде прямоугольников (рис. 11-12), то в формуле (11-74) следует положить k=0 и за производные внутри i-го интервала брать выражения
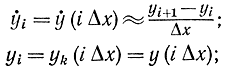
тогда вместо формулы (11-75) получим:
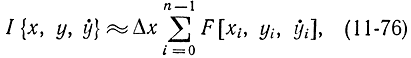
где xi=iΔx.
Пример 11-10. Минимизируем функционал [Л. 77]
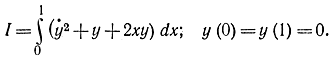
Положим Δx=(1-0)/5=0,2; тогда
y(0)=0; y1=y(0,2), ..., y1=y(0,8); y(1)=0.
В качестве производных примем значения
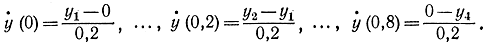
Воспользовавшись формулой (11-76), получим:
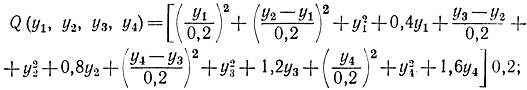
выполнив дифференцирование по yi, имеем:
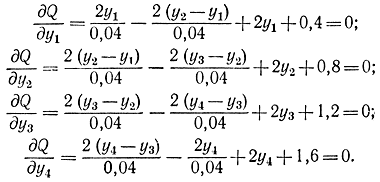
Решениями этих уравнений будут
y1=- 0,0286; y2=-0,0503; y3=-0,0580; y4=- 0,0442.
Точное решение (с точностью до четвертого десятичного знака):
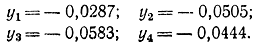
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'