Глава двенадцатая. Непрерывный принцип максимума Понтрягина

Как уже отмечалось, наибольший интерес представляет собой оптимальное управление, связанное с разрывными функциями, составленными из кусочно-непрерывных и кусочно-гладких кривых, содержащих точки с бесконечными значениями первых производных. Наложение ограничений в виде неравенств приводит к образованию среди них участков, состоящих попеременно из внутренних кривых, которые являются экстремалями, и граничных кривых. Переходы между такими участками носят сложный характер.

Распространить на эти случаи методы классического вариационного исчисления оказалось довольно сложно. Было разработано множество частных методов, пригодных для решения узкого класса задач (некоторые из них рассмотрены в предыдущей главе). Однако этих методов возникло чересчур много (чуть ли не свой метод на каждую задачу), а строгость их теоретического обоснования оставляет желать лучшего. Это заставило искать новые общие методы оптимизации, которые, за исключением отдельных случаев, обладали бы достаточной степенью общности и перекрыли бы большинство методов решения вариационных задач.

Одним из таких методов явился непрерывный принцип максимума Понтрягина. Изложение этого метода, к которому мы приступаем, будет дано на уровне инженерной строгости без привлечения аппарата функциональных пространств для случая непрерывных систем управления, поведение которых описывается дифференциальными уравнениями и критерий оптимальности для которых задается в виде функционала. В связи с этим используется термин "непрерывный принцип максимума".

Основная особенность изложения, принятого в данном разделе, состоит в том, что этот метод рассматривается как естественное обобщение и расширение классического вариационного исчисления [Л. 72, 77-81].

Принцип максимума Понтрягина основан на строгой формализации исходной постановки задачи, которая в некоторых деталях отличается от классической постановки Эйлера - Лагранжа и заключается в следующем. Система управления задается уравнениями

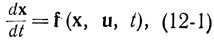
где

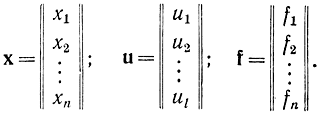
В развернутом виде это векторное дифференциальное уравнение может быть записано так:

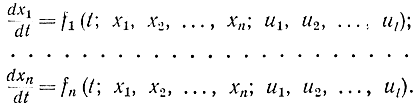
Предположим, что на управление наложено ограничение

или в более общем виде

Требуется определить такое управление u_i, которое обеспечивало бы минимум функционала

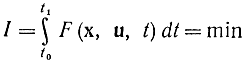
при

Заметим, что случай максимума функционала сводится к отысканию его минимума введением новой подынтегральной функции F₁= - F. Из приведенных формул следует, что в отличие от формализма Эйлера - Лагранжа Понтрягин использует в качестве независимой переменной время t, т. е. рассматривает динамические системы, изменяющие свое состояние во времени. Соответственно для обозначения фазовых координат системы вводятся переменные x вместо y. Далее, в принципе максимума вместо производных от фазовых координат системы ẋ (или ẏ ) используются координаты управления u={u₁,u₂,..., u_l}, а в качестве ограничений выбраны дифференциальные уравнения, описывающие поведение системы (не голономные связи). Правые части этих уравнений зависят в общем от фазовых и управляющих координат и времени t.

Понтрягин особым образом выбирает функцию Гамильтона H и преобразует исходную систему уравнений. Согласно его принципу:

1. преобразованная функция Лагранжа 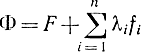не зависит явно от времени. Поэтому формализм Понтрягина допускает существование первого интеграла Эйлера вдоль оптимальной траектории H=const;
2. введенные специально вспомогательные функции ψ₀(t), ψ₂(t),...,ψ₀(t) от которых зависит H, обладают такими свойствами [точнее, одна функция ψ₀(t)] и так входят в H, что вдоль экстремальной кривой H достигают максимума за счет того, что на функцию ψ₀(t) во всех точках экстремальной кривой накладывается ограничение ψ₀(t)≤0;
3. вспомогательные функции ψ_j(t) должны в конце интервала обращать функцию H в нуль, т. е. H(t₁)= 0. Ввиду того что функция H принимает максимальное значение (равное нулю) вдоль кривой, Для которой выполняется условие оптимального управления, этот метод получил название принципа максимума.