12-1. получение уравнений принципа максимума из уравнений Гамильтона-Эйлера

Для лучшего понимания принципа максимума Понтрягина получим его не совсем строгим путем из уравнений Эйлера, или, точнее, Гамильтона - Эйлера. При таком выводе он будет справедлив для тех же случаев, что и уравнение Эйлера, т. е. для непрерывных экстремалей при отсутствии ограничений. В принципе максимума выбирается функция в виде

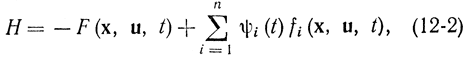
где

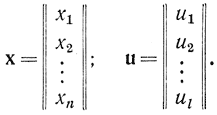
Но при такой записи отсутствует первый интеграл, так как F зависит от t, поэтому вводится новая координата фазового пространства х_n+1=t и новое дифференциальное уравнение системы

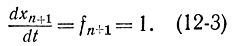
Тогда вместо исходной системы n уравнений

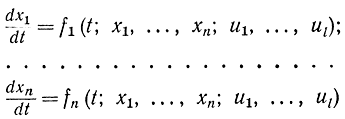
получается система n+1 уравнений:

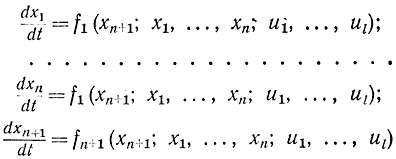
или

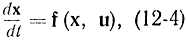
и функция (12-2) записывается как

и функция (12-2) записывается так

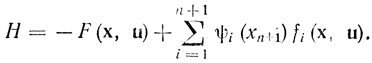
Далее, введя еще одну функцию f₀ и переменную х₀ получаем новое уравнение

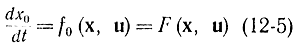
и тем самым сводим задачу к задаче Майера, так как теперь требуется определить такое уравнение, чтобы

при n+2 ограничивающих условиях.

С учетом соотношения (12-5) имеем:

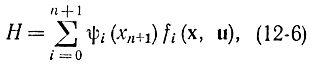
где

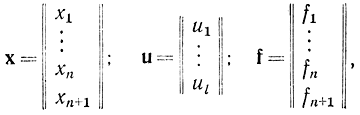
Введя в рассмотрение векторы

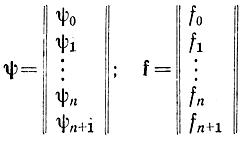
и скалярное произведение, получаем:

Теперь ищем экстремум функционала

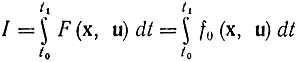
при условиях (12-4). Заметим, что в записи (12-2) функция H Понтрягина не противоречит формализму Гамильтона - Эйлера в вариационной механике. Действительно, в данном случае

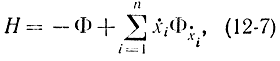
где

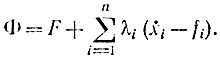
Отсюда

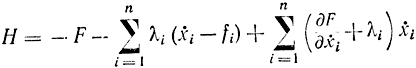
или

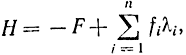
так как

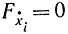
(функция F в принципе максимума от ẋ_i явно не зависит). Эту формулу можно переписать в виде

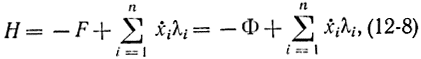
так как в соответствии с уравнениями (12-1) 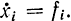Заметим, что, с одной стороны, зависимость Н от F такая же, как Н от Φ, если положить, что 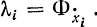. С другой стороны, согласно формализму Гамильтона - Эйлера вводится новая переменная 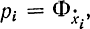, поэтому формула (12-7) записывается в виде

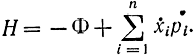
Отсюда, сравнивая полученное выражение с равенством (12-8), приходим к выводу, что

Из изложенного видим, что с самого начала используются вспомогательные функции 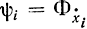с обозначением p_i,- через ψ_i, а так как в соответствии с выражением (12-9) 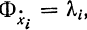,- то

Введение дополнительной фазовой координаты х_n+1 и дифференциального уравнения связи (12-3) дает возможность утверждать, что функция Φ не зависит от времени и что существует первый интеграл Эйлера

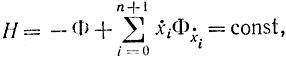
т. е. Н=(ψ, f) сохраняет постоянное значение на оптимальной траектории.

Докажем теперь, что вдоль этой траектории Н удовлетворяет уравнениям Гамильтона - Эйлера:

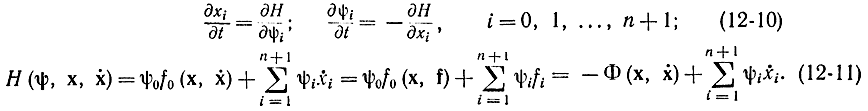
Можно утверждать, что уравнения (12-10) являются необходимыми условиями экстремума функционала (12-7) при ограничениях (12-5), так как мы проследили и убедились, что формализм Гамильтона - Эйлера соблюдается. Первое уравнение (12-10) получим прямым дифференцированием уравнения (12-11) по ψ_i с учетом того, что 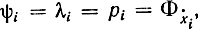ψ₀=-1, f₀=Φи 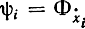не зависит от ẋ_i,и поэтому

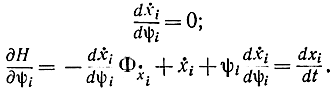
Второе уравнение (12-10) получим дифференцированием уравнения (12-11) по x_i

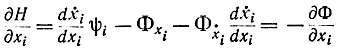
аналогично выводу уравнения Гамильтона-Эйлера, после чего используем уравнение Эйлера

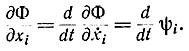
Следует заметить, что наш вывод может вызвать сомнения в части использования новой переменной 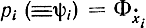при выводе уравнений Гамильтона -Эйлера для замены переменной ẋ_i в функции

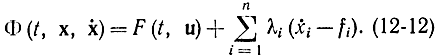
Функция F от ẋ не зависит (здесь специально выбрана такая форма функционала), а сумма в выражении для Φ зависит от ẋ_i линейным образом, в силу чего нет зависимости Φ _ẋi от ẋ_i поэтому нельзя выразить ẋ_i как функцию p_i=ψ_i принципе максимума по существу специально избегают этой зависимости (за счет формализма исходной постановки задачи) и специальными приемами, отличными от метода Гамильтона - Эйлера, доказывают, что уравнения (12-10) обеспечивают экстремум исходного функционала. Такой формализм тем более оправдан, что большинство задач оптимального управления сводится к вырожденным функционалам, подынтегральные выражения в которых (даже при формализме Эйлера - Лагранжа) не зависят от ẋ_i. Так, в задаче о максимальном быстродействии

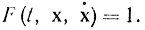
Однако вывод уравнений Гамильтона - Эйлера остается справедливым и в нашем случае при независимости Φ _ẋi от ẋ_i и без требования выразить ẋ_i через ψ_i(=p_i=λ_i,), так как Φ _ẋi сразу заменяется на ψ_i=λ_i=p_i. В отличие от вывода уравнения Гамильтона - Эйлера при этом не вводится функциональной связи между ẋ_i и ψ_i благодаря формализму принципа максимума и, в частности, тому, что функция F не зависит от ẋ_i поэтому ,

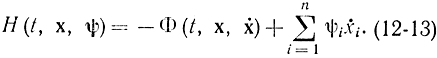
Дифференцируя формулу (12-13) по ψ_i, получаем:

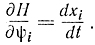
Это - первое уравнение метода Понтрягина. Далее, дифференцируя формулу (12-11) по ẋ_i получаем:

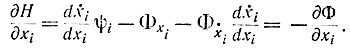
Здесь необходимо учитывать, что 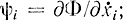кроме того, при дифференцировании следует различать частные и полные производные. Далее, используя уравнение Эйлера, имеем:

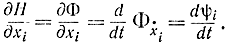
Это - второе уравнение метода Понтрягина.

Здесь напрашивается параллель с минимаксной трактовкой уравнений Гамильтона - Эйлера (см. § 11-9). Если сформулировать аналогичные результаты для постановки задачи оптимизации по методу Понтрягина и рассматривать x_i(t) и ψ_i(t)[=p_i(t)] как независимые переменные, то каждое уравнение (12-10) представляет собой уравнение Эйлера для функционала

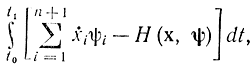
а фазовые траектории, удовлетворяющие уравнениям (12-10), представляют собой решения минимаксных задач

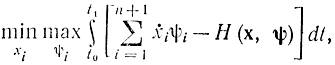
где

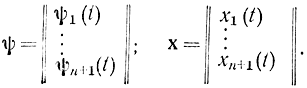
Как уже указывалось в параграфе 11-9, если считать ψ_i(t) и x_i(t) независимыми переменными, го бессмысленно говорить об экстремуме функционала. При выводе уравнений Понтрягина на стадии дифференцирования по существу предполагалось, что x_i и ψ_i,- явно x_i и ψ_i друг от друга не зависят. И только использованием уравнений Эйлера при получении второго уравнения Понтрягина была введена связь переменных x_i и ψ_i. Благодаря этому в методе Понтрягина функции x_i и ψ_i связываются системой линейных дифференциальных уравнений, получаемых в результате подстановки выражения для Н во второе уравнение (12-10).

В функцию Н [см. (12-11)1 явным образом не включены переменные управления u_v, и для них нет соответствующих уравнений Гамильтона - Эйлера в системе (12-12), что имеет следующее объяснение. Здесь рассматриваются такие функционалы, которые не зависят от производных управляющего сигнала, поэтому

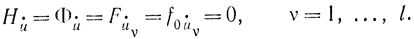
Отсюда обобщенные импульсы для функций управления

p_i=ψ_i=λ_i=0, i=n+2, ...,n+l+2

и соответствующая пара уравнений Гамильтона-Эйлера для этих переменных вырождается в одно из уравнений вида

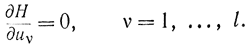
Хотя эти уравнения и не включены в основные уравнения (12-10), их используют для определения параметров оптимального управления.

Рассмотрим еще один способ изложения принципа максимума [Л. 77]. Допустим, ищется минимум функционала

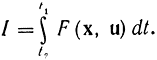
Положим

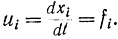
Такой заменой задача сводится, по существу, к классической постановке Эйлера - Лагранжа, когда подынтегральная функция в функционале зависит от производных фазовых координат. Именно на основе результатов классического вариационного исчисления доказывается, что функция Понтрягина Н принимает при оптимальном управлении максимальное значение. Очевидно, что наш вывод справедлив при соблюдении условий классического вариационного исчисления. В соответствии с изложенным функция Понтрягина принимает вид:

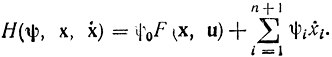
Разложим функцию И в ряд Тейлора по переменной ẋ_i=u:

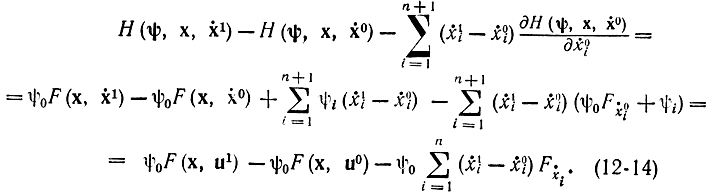
Если число функций x_i равно единице, на основании формулы (12-14) получим:

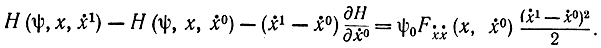
В случае минимума функционала согласно необходимому условию Лежандра

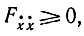
поэтому, учитывая, что ψ₀ <0, получаем

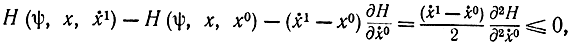
откуда следует, что

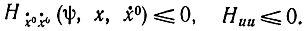
Учитывая, что необходимым условием достижения экстремума функцией Н относительно ẋ является равенство нулю производной по этой переменной

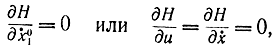
получаем:

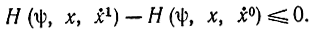
Тем самым доказано, что на оптимальной кривой функция Н достигает максимума.

Функции ψ_i в принципе максимума выбираются так, чтобы

где Т=t₁ Поэтому Н - отрицательная функция, достигающая максимального значения, равного нулю. Нетрудно убедиться, что два уравнения Понтрягина (12-10) неравноценны: первое сводится к исходным уравнениям движения и не содержит условий экстремума, второе содержит условие экстремума функционала.

Вариационная задача в методе Понтрягина сводится к нахождению n функций ψ_i i=1, 2,..., n, которые определяются из дифференциальных уравнений, получаемых из второй группы уравнений (12-10), если в них подставить выражение (12-6) для Н:

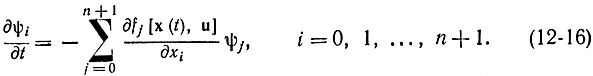
Это линейные дифференциальные уравнения в обычных (не частных) производных. Всего в рассмотренной задаче неизвестных функций 2n+4+l:n+2 функций x_in+2 функций ψ_i, l функций управления u_i и соответственно n+2 дифференциальных уравнений, описывающих поведение системы, n+2 линейных сопряженных уравнений (12-16) и l уравнений, которые вытекают из того, что вдоль оптимальных кривых

При достижении экстремума внутри области |u_i|≤1 условие (12-16) дает l уравнений:

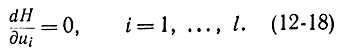
В случае, когда управление одно, условие (12-17) сводится к dH/du=0. Если экстремум функционала достигается на какой-нибудь грани n-мерного параллелепипеда, определенного соотношением |u_i|≤1, то одно из l необходимых уравнений вытекает из принадлежности управления u(t) этой грани; остальные l-1 условий появляются в результате приравнивания нулю частных производных от Н по l-1 направлениям в этой грани. Если имеется случай трехмерного пространства l=3, то грань является плоскостью в трехмерном пространстве. В этой плоскости имеются два независимых направления, по которым и следует брать производные от Н. Таким образом, условие (12-18) всегда содержит l уравнений. Практически всегда сначала определяют х(t,u) и ψ(t, u), зависящие от неизвестных управлений и, а затем определяют оптимальные управления.

В принципе максимума есть одна трудность: решить уравнения (12-10) возможно лишь при наличии 2n+2 начальных условий. Для x_i(t) они заданы:

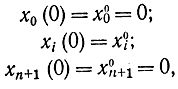
но для функции ψ_i(t) заданы только конечные условия. Так, в случае задачи с закрепленными концами (t₀, t₁=Т заданы) конечные условия имеют вид:

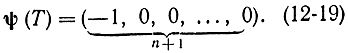
Значение ψ_n+1(T)≠0 и определяется соотношением (12-15). Поэтому

0 простейшем случае поступают по методу "пристрелки": задаются какими-то начальными значениями для ψ_i,- и при заданных начальных значениях для x_i рассчитывают траекторию. Если она удовлетворяет условиям (12-19), процесс вычислений заканчивается, если не удовлетворяет, процесс вычислений повторяют для новых ψ_i(0).

Рассмотренный метод вывода уравнений Понтрягина из уравнений Эйлера - Лагранжа справедлив при условии, что функционал - не особый и справедливы положения классического вариационного исчисления, в частности уравнение Эйлера. Такая ограниченность метода не дает возможности рассматривать самые важные для кибернетики случаи с бесконечными значениями производных от функции управления. Однако известны другие методы для обоснования и доказательства принципа максимума, отличные от классического вариационного исчисления.