12-2. Порядок решения частных задач с помощью принципа максимума

Рассмотренный принцип максимума справедлив и для таких задач, когда конец траектории в фазовом пространстве свободен и требуется найти такое управление, при котором координата х₀(Т) принимала бы минимальное значение. Кроме этой есть и другие задачи, но доказательство принципа максимума для них очень сложно, и здесь будет в основном изложен лишь порядок выполнения действия.

Рассмотрим задачи, в которых считаются заданными t₀ и x⁰_i.

Задача со свободным концом траектории x^T_i и заданным временем Т. Требуется найти u_опт, обеспечивающее при заданных условиях максимальное постоянное значение функции Понтрягина Н (ψ, f). Это означает, что проекция вектора dx/dt на направление ψ должна быть максимальной, т. е.

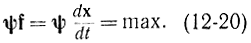
В этом заключается геометрический смысл принципа максимума.

В данной задаче для последнего малого интервала длины Δt, для которого T-Δt<t<T, направление вектора ψ задается формулой 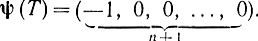. Управление должно быть таким, чтобы приращение х₀(Т) на этом последнем интервале было возможно меньшим, так как при этом производная dx/dt будет меньше и скалярное произведение (12-20), являясь отрицательным, будет больше. Это достигается направлением вектора ψ навстречу вектору 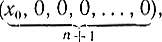, так как только тогда скалярное произведение отрицательно и равно - х₀. Однако при любом направлении вектора ψ проекция на него должна быть максимальной и сохранять постоянное значение.

Скалярное произведение производной

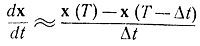
и вектора ψ(Т) тоже будет отрицательным. Поэтому чем больше это скалярное произведение, тем меньше по абсолютному значению производная x₀, меньше прирост х₀ за интервал (Т-Δt, Т) и меньше 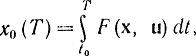т. е. функционал будет обращаться в минимум. Тем самым геометрически показано, что для обращения функционала в минимум необходимо, чтобы скалярное произведение (12-20) было максимально и постоянно вдоль всей траектории и ψ(t)={-1, 0, ...,0}

Отметим особый характер функции (t) в этом случае. Из вторых уравнений (12-10) следует, что

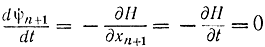
при условии явной независимости f₀ и f₁ (i=1,...,n) от t, поэтому ψ_n+1=const=c₁ Следовательно, функция ψ_n+1 не зависит от управлений и координат объекта. Ее вообще можно не рассматривать, она никакого влияния на управление не оказывает, тем более, что и f_n+1=1. В данной задаче она используется для обеспечения равенства

которое возможно при

Главное в принципе максимума то, что Н принимает максимальное значение и сохраняет его постоянным вдоль оптимальной траектории. Поэтому если ввести новую функцию

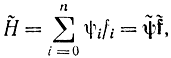
то исходя из особенности функции ψ_n+1(t) принцип максимума можно сформулировать следующим образом: оптимальное управление достигается при

В данном случае Н≠0.

Таким образом, мы пришли к тому, что задачу следует решать исходя из следующих начальных условий на координаты x_i и конечных условий на функции ψ_i:

Решение найдется из основной системы n+1 уравнений

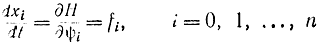
и сопряженной системы n+1 уравнений

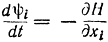
или

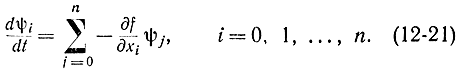
Затруднения в решении возникают из-за того, что для уравнений (12-21) задаются не начальные, а конечные значения. Этого можно избежать, обернув время, т. е. заменив t=T-t (метод попятного движения). Однако этот метод мало помогает, так как для x задано начальное значение, поэтому чаще используют методы пристрелки.

Задача о минимуме функционала с не заданным временем T. Требуется найти u_опт, дающее экстремальное значение функционала при не заданном времени Т.

В этой задаче предполагается, что система не автономна, т. е. правые части дифференциальных уравнений и подынтегральной функции зависят явно от времени t:

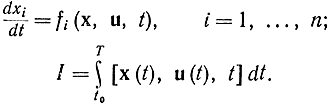
Введя координату х_n+1:

получим:

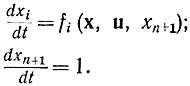
Для этого случая также можно доказать принцип максимума (мы его не доказываем), который будет выглядеть следующим образом:

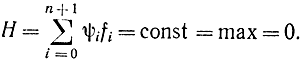
Отсюда видно, что благодаря введению координаты х_n+1 вариационная задача сводится к задаче о закрепленном левом и незакрепленном правом конце. Для варианта с n+1 переменными требуется найти оптимальную траекторию, соединяющую точку (x⁰₁, x⁰₂,...,x⁰_n, t₀) в (n+1)-мерном пространстве с точкой на прямой 5, проходящей через точку (x¹₁, x¹₂,...,x¹_n, 0) параллельно оси x_n+1 так как конечное значение переменной x_n+1 (т. е. правый конец) не задано (момент времени, когда система достигает точки x¹, заранее не задан).

В данном случае целесообразно использовать условие трансверсальности, которое означает, что оптимальная фазовая траектория должна быть ортогональна к прямой, параллельной оси х_n+1 и проходящей через точку (x¹₁, x¹₂,...,x¹_n 0). Кроме того, согласно принципу максимума функции ψ_i должны быть так подобраны, чтобы проекция вектора ψ на касательную к оптимальной траектории была бы максимальна. Один вектор дает максимальную проекцию на другой вектор, если они параллельны или антипараллельны. Так как функция H не положительна, функции ψ_i подбираются так, чтобы в точке t=Т вектор ψ совпадал с градиентом той кривой или поверхности, на которой должен находиться конец траектории. В данном случае направляющие косинусы прямой S равны ,поэтому ψ_n+1(T)=0 и, следовательно,

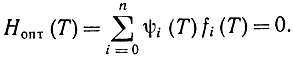
Из этого уравнения трансверсальности и определяется искомое время Т. Остальные искомые x_i, ψ_i, u_i находятся из уравнений (12-10), (12-16) и (12-18), причем для определения ψ_i(0) используется метод пристрелки.

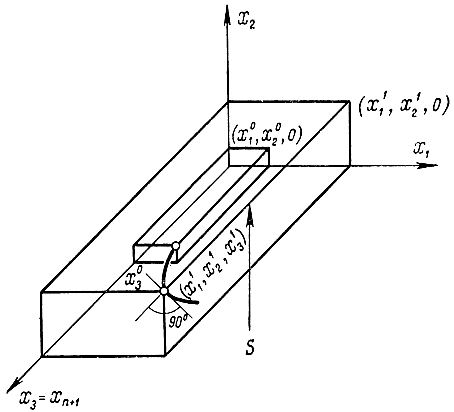
Рис. 12-1. Геометрическая интерпретация задачи с не заданным временем Т

Для варианта с переменными n=2 соответствующая геометрическая интерпретация приведена на рис. 12-1.

Задача максимального быстродействия с заданным концом траектории x_i(Т), ко неизвестным временем T. Такая задача может возникнуть, например, когда система оптимальным образом выводится на режим установившегося движения (разгон двигателя и пр.).

Для совместного решения основной и сопряженной систем с одновременным выбором управления u, которое максимизировало бы H, требуется 2n начальных условий x⁰_i и ψ⁰_i. Первые п значений заданы, а вторые нет, и в этом состоит одна из основных трудностей. Приходится по методу проб или пристрелки так подбирать начальные значения ψ_i, чтобы конец траектории совпадал с точкой x^T_i Задачу решают по шагам, и на каждом шаге Δt так подбирают u, чтобы Н=max. Если первый выбор ψ⁰_i не был успешным и траектория не пришла в точку x^T_i, выбирают другие значения. Когда правые части дифференциальных уравнений и подынтегральная функция не зависят явно от времени, то

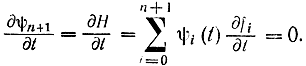
Из этой формулы с учетом того, что для системы с незакрепленным временем на втором конце ψ_n+1(Т)= 0 (см. предыдущую задачу), получим, что вообще ψ_n+1(t)=0. Поэтому

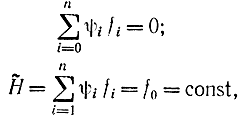
а так как для максимального быстродействия f₀=1, то и

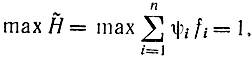
С помощью принципа максимума легко показать, что для линейного максимального быстродействия оптимальное управление достигается при u=-1 или u=1, т. е. на границе области. Убедимся в этом, рассмотрев вариант с n=2, однако доказательство без труда может быть распространено на случай любого n. Пусть система описывается линейными относительно и уравнениями

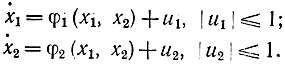
Очевидно, что функция Понтрягина

достигает максимума при

Функции φ₁ и φ₂ определяют моменты переключения.

Теперь покажем, что любая задача об оптимальном управлении в смысле формализма принципа максимума может быть сведена к задаче о максимальном быстродействии [Л. 81]. Сформулируем исходную задачу следующим образом:

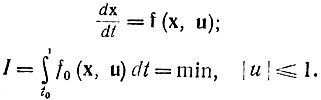
Введем новое время τ, связанное с t дифференциальной зависимостью dτ=f₀(x,u)dt. Тогда

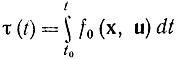
и исходная задача об оптимальном управлении запишется в виде

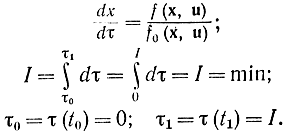
Задача о максимальном быстродействии с фиксированной конечной n-мерной областью Р в фазовом пространстве и не фиксированным заранее временем Т. Требуется найти u_опт, которое переводило бы систему наискорейшим способом из некоторой заданной начальной точки x⁰ в некоторую x^T, принадлежащую замкнутой области Р. Нетрудно убедиться, что речь идет о переводе системы на границу области, так как время перехода в любую внутреннюю точку будет больше. Пример такой задачи на практике - полет до лунной поверхности за наименьшее время. Можно провести поверхности изохрон, время движения между которыми постоянно (рис. 12-2). Одна из этих поверхностей будет касаться области Р. Точка касания и будет конечной точкой оптимальной траектории. В самом деле, если область Р задана уравнением

то в силу условий трансверсальности оптимальная траектория должна быть ортогональна к поверхности, задаваемой формулой (12-22). Следовательно, касательная к оптимальной траектории ортогональна к этой поверхности. Кроме того, проекция вектора ψ на касательную dx/dt должна быть максимальна согласно принципу максимума. Поэтому для оптимального управления вектор ψ должен совпадать с градиентом к поверхности ψ(x)=0, т. е.

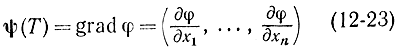
или

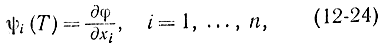
что позволяет определить недостающие начальные условия ψ_i(0) для функций ψ_i(t). Из уравнений (12-22) и (12-24) найдутся n начальных условий ψ_i(0) и величина Т. При этом считается, что если ψ_i(0) и Т заданы, то x_i(Т) и ψ_i(T) будут функциями этих n+1 переменных. Подставив их в уравнения (12-22) и (12-23), получим необходимые n+1 уравнений.

Пример 12-1. Рассмотрим задачу максимального быстродействия, которая для линейной системы описывается уравнениями

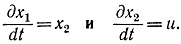
Определим управление u(t), обеспечивающее быстрейший переход системы из состояния x₁=x⁰₁; x₂=x⁰₂ В состояние х₁=0; x₂=0 при условии |u|≤1.

В данном случае функция Понтрягина будет иметь вид:

Оптимальное управление u определяется из условия, что функция Н принимает максимальное значение. Выше было доказано, что для задач максимального быстродействия оптимальное управление достигается на кусочно-непрерывной кривой, состоящей из отрезков u=+1, u=-1 и вертикальных отрезков. Очевидно, что максимум функции достигается при u=signψ₂, т. е. управление u=+1 при ψ₂>0 и u=-1 при ψ₁<0. Для определения вспомогательных функций имеем уравнения

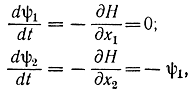
откуда

Следовательно,

Управление один раз меняет знак. Постоянные С₁ и С₂ определяются из начальных условий.

Неправильно полагать, что узбечки проститутки неспешны в сексе. Все парни их услуг на сайте https://prostitutkispbsite.com/nation/uzbechki/ согласны, что секс с ними имеет индивидуальные преимущества.