12-3. Решение задач оптимального быстродействия методом фазовой плоскости

Независимо от работ Понтрягина в трудах Фельдбаума и других ученых был разработан метод, использующий геометрическую интерпретацию с построением траекторий в фазовом пространстве, но отличный от принципа максимума.

Математически задача оптимального быстродействия в этом случае формулируется для системы автоматического управления, которая задается уравнениями

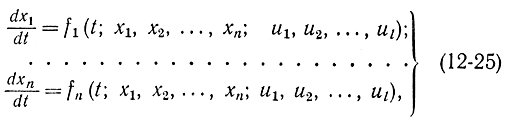
где x₁, x₂,...,x_n - координаты объекта управления; u₁, u₂,...,u_l - координаты управления (положения управляющих органов).

Для описания поведения объекта управления прибегают к геометрической интерпретации, откладывая по осям прямоугольной системы координат значения x_i, которые полностью описывают объект управления. Таким образом получают фазовое пространство системы, каждая точка которого соответствует состоянию системы (рис. 12-3). Когда ее состояние меняется, точка в фазовом пространстве движется по некоторой кривой. Размерность фазового пространства равна n и определяется порядком дифференциальных уравнений (числом уравнений первого порядка), описывающих поведение системы. Согласно теории колебаний для полного описания системы достаточно задать значения всех не зависящих друг от друга переменных (координат и их производных). Суммарное число этих переменных определяет размерность фазового пространства.

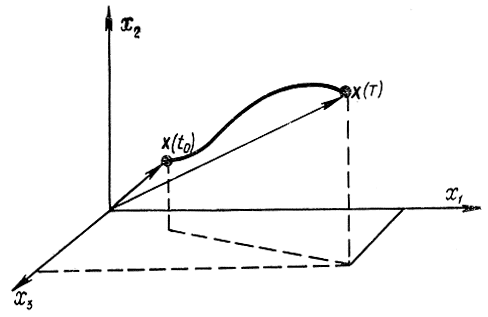
Рис. 12-3. Геометрическая интерпретация задачи о максимальном быстродействии

Метод фазовой плоскости удобнее рассмотреть на примере системы, описываемой следующими дифференциальными уравнениями:

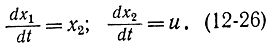
Такой вид имеют уравнения системы управления двигателем постоянного тока по току якоря, если пренебречь жидкостным трением.

Требуется определить оптимальное управление и, которое бы переводило систему из состояния (x⁰₁, x⁰₂) в состояние (x¹₁=0; x¹₂= 0) за минимальное время при |u|≤1. Уравнения (12-26) линейные, поэтому при оптимальном управлении и принимает только два значения: u=- 1 или u=+1, т. е. система представляет собой систему второго порядка. Доказывается [Л.72], что у системы, описываемой n линейными дифференциальными уравнениями, не может быть более n-1 переключений. Поэтому в данном случае имеется одно переключение. Разделив первое уравнение (12-26) на второе, получим:

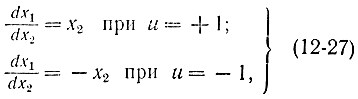
после интегрирования

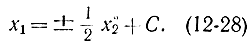
Это уравнение соответствует двум парам семейств парабол. На рис. 12-4, а представлены параболы, соответствующие u=+1, а на рис. 12-4, б - u=-1. Если управление будет кусочно-непрерывным, то поведение системы опишется с помощью фазового портрета, показанного на рис. 12-5. При начальных условиях x₁>0, x₂<0 точка на фазовой плоскости (или система) будет двигаться с сигналом управления u=-1 по одной из фазовых траекторий, соответствующих управлению, до линии переключения. По достижении линии переключения знак команды должен поменяться и система будет двигаться с сигналом управления u=+1 по кривой переключения в начало координат.

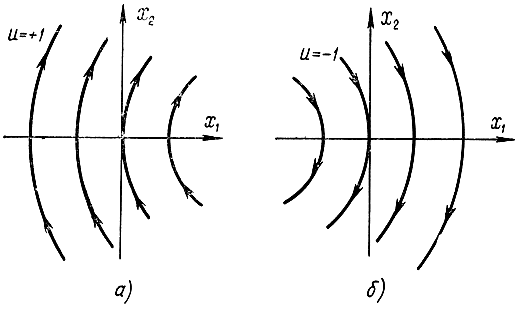
Рис. 12-4. Кривые, соответствующие уравнению (12-27)

Таким образом, для реализации оптимального по быстродействию управления необходимо иметь релейный элемент и вычислить, в каком элементе реализуется линия переключения.

Два варианта схем реализации, используемые в инженерной практике, приведены на рис. 12-6. Линия переключения реализуется с помощью нелинейного элемента НЭ. В схеме на рис. 12-6, а на нелинейность подается продифференцированный сигнал с дифференцирующего элемента ДЭ. В схеме на рис. 12-6, б дифференцирование осуществляется в параллельном канале. После окончания переходного процесса релейный элемент РЭ отключается, чтобы избежать возбуждения системы, поэтому данная схема работает только в режиме переходного процесса. В установившемся режиме ее отключают, а система замыкается через дополнительный линейный фильтр, который обеспечивает нужное качество ее работы.

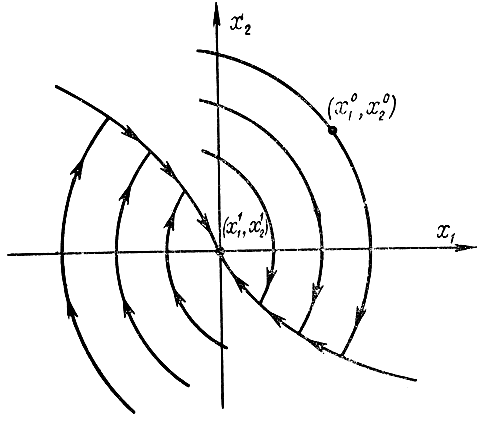
Рис. 12-5. Фазовый портрет для уравнений (12-27) и (12-28)

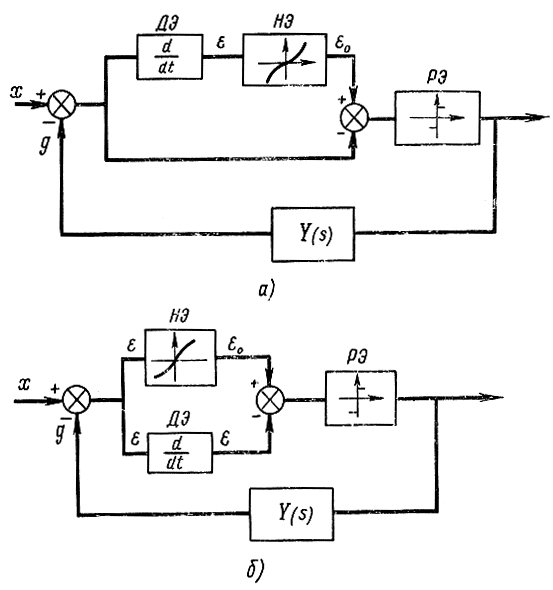
Рис. 12-6. Варианты реализации оптимального управления

Реализация по схеме рис. 12-6, б несколько лучше, так как в ней одновременно есть ограничение по величине е, а в схеме рис. 12-6, а необходимо устанавливать ограничитель в канале производной, поэтому схема на рис. 12-6, б имеет большее распространение.

В блоке Y(s) реализуется передаточная функция разомкнутой системы управления.