13-1. Принцип оптимальности

В основе непрерывного и дискретного динамического программирования лежит принцип оптимальности Веллмана, который заключается в следующем [Л. 72, 80]. Допустим, требуется определить функцию y(x) обращающую в минимум функционал

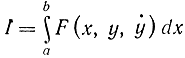
при условии

Рассмотрим в фазовом пространстве оптимальную траекторию y_ay₀y_b (рис. 13-1). Разделим ее на два участка, обозначенные цифрами 1 и 2. Будем для простоты пока считать, что y_b фиксирован. Принцип оптимальности утверждает, что если вся траектория оптимальна, то участок 2 тоже оптимален. Это значит, что если начальное состояние системы определяется y₀ при х=х₀, то независимо от того, по какой траектории система пришла в эту точку, ее дальнейшее движение будет происходить по участку 2. Такая независимость последующего движения от предыстории является характерной особенностью случайных марковских процессов без последействия.

Если допустить, что участок 2 не является оптимальным, то существует другой участок 2' с началом в точке y₀, который будет оптимальным. Но тогда вместо начальной траектории 1-2 существует другая траектория 1-2'у на которой достигается экстремум. Это противоречит исходному предположению о том, что траектория 1-2 оптимальна.

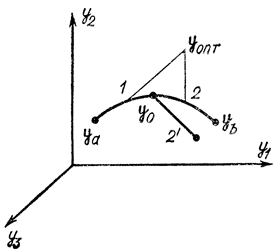
Рис. 13-1. Пояснение к принципу оптимальности Беллмана

Заметим, утверждение о том, что любой участок оптимальной траектории есть оптимальная траектория, с некоторой точки зрения неверно. Действительно, если задана только начальная точка y_a, то участок 1 траектории 1-2 может и не быть оптимальным. Приведем пример. Пусть требуется оптимальным образом распределить темп бега спортсмена на дистанции от y_a до y_b так, чтобы он за минимальное время достиг точки y_b. Очевидно, что если дистанция достаточно большая, то тренер бегуна вряд ли даст ему указание бежать на каждом участке как можно быстрее. Бегун должен оптимальным образом составить свой график бега из расчета пробега всего пути в целом от y_a до y_b за минимальное время. Так, он может вначале бежать не в полную силу, чтобы обеспечить бурный финиш. Совсем другое дело, если бегуну зададут конечную точку y₀ и скажут, чтобы он наилучшим образом пробежал Дистанцию 1 у т. е. первый участок будет оптимален, когда помимо начальной точки y_a задана еще и конечная точка интервала y₀. В связи с этим целесообразно напомнить, что обычная экстремаль (в случае невырожденного функционала) представляет собой как бы единую цепь, каждое звено-участок которой является также экстремалью. По существу, Беллман с помощью принципа оптимальности расширил класс допустимых экстремалей, потребовав, чтобы только конечный участок оптимальной траектории был оптимален.

Это условие оптимальности определяет масштабы применяемости принципа максимума. Если оно несправедливо, то решать задачу с помощью динамического программирования нельзя.

Часто удается свести исходный процесс к новому путем увеличения числа измерений фазового пространства, и для такого процесса условие оптимальности будет выполняться.

Заметим, что принцип оптимальности справедлив и для дискретных, и для стохастических процессов управления, которые будут рассмотрены в отдельности. Условие оптимальности сразу позволяет получить основные уравнения метода динамического программирования - функциональное и дифференциальное уравнения Беллмана.