13-2. Функциональное уравнение Беллмана

Вернемся к функционалу

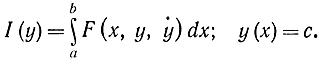
Минимум его зависит от а и с. Введем обозначение

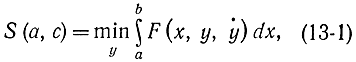
где -∞<a<c; -∞<c<∞. В силу аддитивности интеграла можем написать

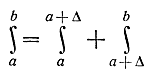
и, применив принцип оптимальности, получим:

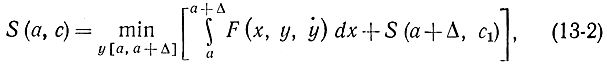
где минимизация производится по всем y(х), определенным на промежутке изменения x∈[a, a+Δ], причем

Нетрудно убедиться, что функциональное уравнение Беллмана представляет собой формальную запись принципа оптимальности, состоящего в поэтапном определении оптимального управления: вначале ищется минимум на конечном участке 2, затем на всей траектории 1-2 (см. рис. 13-1).

Функциональное уравнение дает по существу рекуррентные соотношения для решения оптимальных задач численным методом на ЦВМ. Но на данном этапе нас это уравнение интересует с той точки зрения, что оно позволяет получить дифференциальное уравнение Беллмана и все основные соотношения классического вариационного исчисления.