13-3. Дифференциальное уравнение Беллмана

Если задано, что y(а)=с, то выбор функции y(х) на интервале [а, а+Δ] эквивалентен выбору y(х) на интервале [а, а+Δ]. Если Δ мало, а y(х) непрерывна, то выбор ẏ(х) на интервале [а, а+Δ] эквивалентен выбору y(а). Если отбросить члены малости выше первого порядка относительно Δ, то нетрудно убедиться в справедливости следующих соотношений:

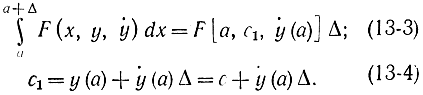
Вводя обозначение

и подставляя выражения (13-3) и (13-4) в функциональное уравнение (13-2), получаем:

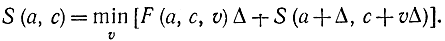
Разложив функцию S(a+Δ, с+vΔ) в ряд Тейлора

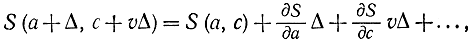
в пределе при Δ→0 получим нелинейное дифференциальное уравнение в частных производных:

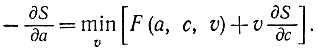
Это и есть знаменитое уравнение Беллмана. Оно справедливо для любого значения а=х, поэтому его можно переписать в виде

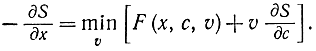
Если ввести вместо х время t, с заменить на x и выделить координату управления u, которую необходимо определить оптимальным образом, то задача нахождения минимума функционала

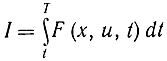
сведется к решению уравнения

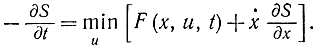
Наконец, если имеется несколько координат и управлений (векторное управление), то задача минимума функционала

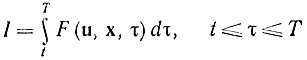
сведется к решению следующего дифференциального уравнения:

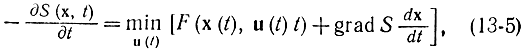
где

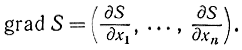
Если система описывается n дифференциальными уравнениями первого порядка

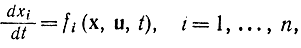
то уравнение (13-5) запишется в виде

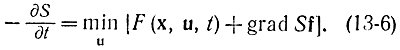
Дифференциальное уравнение Беллмана является своеобразным нелинейным дифференциальным уравнением. В нем обязательно присутствует операция минимизации. В случае уравнения вида (13-6) минимум берется по u:

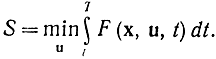
После того как сделан перебор по всем и и выбрано оптимальное управление, правая часть уравнения (13>6) не зависит от u. Вывод уравнения (13-6) требовал, дифференцируемости и существования частных производных от функции S по всем переменным t, x_i. Однако можно привести много примеров, где функция не является дифференцируемой, а оптимальное управление существует. Можно показать, что на линии переключения функция всегда не дифференцируема. Поясним это на примере [Л. 81].

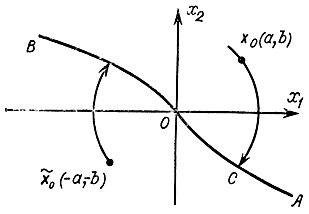
Рис. 13-2. Пояснение к примеру 13-1

Пример 13-1. Рассмотрим систему дифференциальных уравнений:

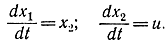
Решив их при u=±1, получим выражение для фазовых траекторий в виде

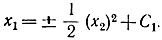
Линия переключения получается при С₁=0.

Пусть начальная точка х₀ лежит выше линии переключения (рис. 13-2) и имеет координаты (a, b). Из условия прохождения параболы через эту точку находим:

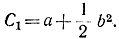
Уравнение самой параболы имеет вид:

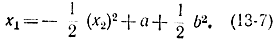
Для определения точки переключения С необходимо решить совместно уравнение (13-7) и уравнение линии переключения

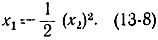
Вычитая уравнение (13-8) из (13-7), получаем:

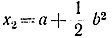
или

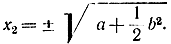
Для точки С надо взять знак минус, тогда

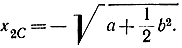
При движении от точки х₀ до точки Сu=-1, поэтому х₂=-1. Интегрируя это уравнение, получаем:

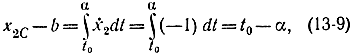
где α - момент переключения. Аналогично при движении от точки С до начала координат u=1, ẋ₂= 1 и

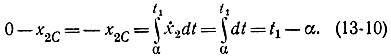
Вычитая из уравнения (13-10) уравнение (13-9), получаем:

Это - минимальное время движения по оптимальной траектории:

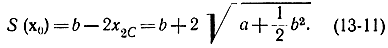
Так же можно вычислить эту функцию для случая, когда начальная точка лежит ниже линии переключения (х₀ на рис. 13-2). Однако из геометрических соображений следует, что если поменять а на -а и b на -b, то оптимальное время будет то же самое. Поэтому для. случая, когда x₀ лежит ниже линии переключения, траектория

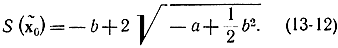
Для хо, лежащих на линии переключения (ниже начала координат),

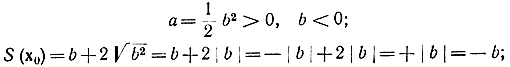
для точек х₀, лежащих выше начала координат,

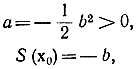
т. е. функция S непрерывна везде и имеет вид:

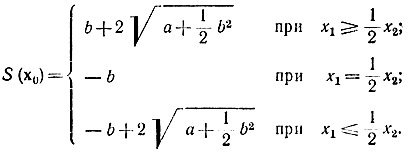
Покажем, что хотя эта функция и непрерывна, у нее нет производных по х на линии переключения. Пусть точка С с координатами (a₀, b₀) (рис. 13-3) лежит на дуге A0 так, что a₀=(b_0²/2 и b₀<0

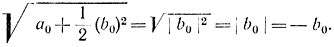
Определим производные от S, функции задаваемой формулой (13-11)

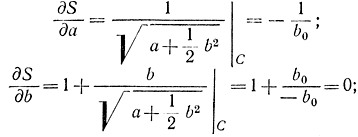
для формулы (13-12)

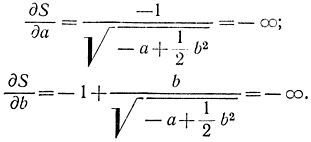
Как видим, при смещении из точки С вверх dS/db=0, при смещении вниз dS/db=-∞, т. е. производной dS/db в точке С не существует. Так же не существует в точке С производной dS/da.

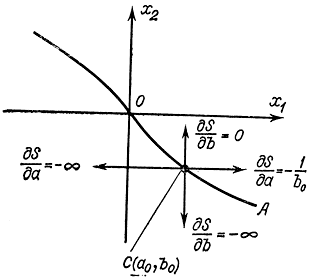
Рис. 13-3. Пояснение к не дифференцируемости функции Белламана на линии переключения

Тем самым показано, что на линии переключения производных от S не существует. В остальных точках плоскости эта функция дифференцируема. Так как фазовая траектория обязательно содержит участок линии переключения,то для рассматриваемого случая нельзя написать дифференциальное уравнение Беллмана, если использовать рассмотренный ранее вывод этого уравнения. Однако можно вывести дифференциальное уравнение Беллмана другим способом [Л. 82, 83], при котором не требуется выполнения условия дифференцируемости функции Беллмана. При этом достаточно непрерывности скалярного произведения gradSf (t, х, u), что в большинстве случаев справедливо для линии переключения.