13-4. Динамическое программирование и принцип максимума

Получим из динамического программирования принцип максимума [Л. 72]. Для этого соответствующим образом формализуем задачу, т. е. опишем систему уравнениями

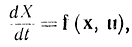
где

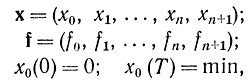
и введем (n+2)-мерную вектор-функцию

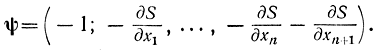
Тогда дифференциальное уравнение Беллмана

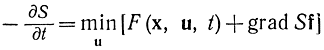
с учетом того, что min(+μ)=-max(-μ) [например, min (3,5)=-max(-3, -5)], запишется в виде

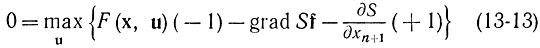
или

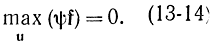
Теперь, если ввести функцию

из выражения (13-14) получим принцип максимума Понтрягина:

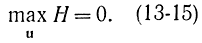
Чтобы вывести дифференциальные уравнения принципа максимума, предположим, что функция S(x) имеет вторые производные по всем x_i. В соответствии с выбором функций ψ_i для производной от них по времени имеем:

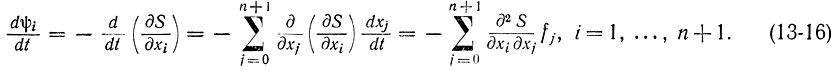
Очевидно, что если ψ₀=-1, то dψ₀/dt=0. Согласно формуле (13-15) для оптимального управления u_опт(t) имеем:

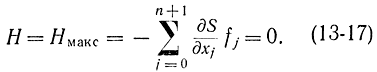
Рассмотрим фиксированный момент времени t, для которого u_опт(t) тоже будет фиксированной величиной. Для точек пространства х, отличных от той, которая лежит на рассматриваемой траектории, данное управление u_опт уже не будет оптимальным, и для них величина Н не будет достигать своего максимума, поэтому при фиксированных t и u_опт(t) величина H=ψf достигает своего максимума, равного нулю, относительно координат x_i именно в точке оптимальной траектории и, следовательно, в этой точке производные от Н по x_i обращаются в нуль. Продифференцировав соотношение (13-17) по x_i, получим:

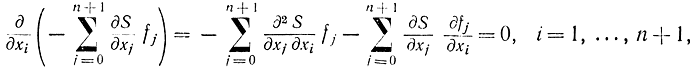
откуда

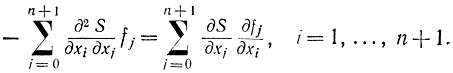
Сравнивая это соотношение с (13-16), замечаем, что его левая часть совпадает с правой частью (13-16), поэтому

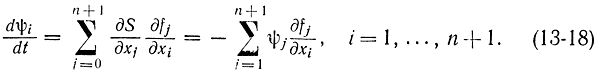
Это и есть сопряженные уравнения принципа максимума. Если продифференцировать

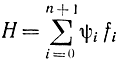
по x_j и сравнить полученное выражение с (13-18), то можно получить:

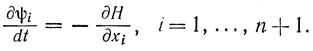
Далее, дифференцируя формулу (13-18) по ψ_j, имеем:

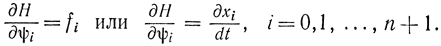
Таким образом, видим, что получены оба уравнения Понтрягина.