13-5. Геометрическая интерпретация динамического программирования

Оптимальное управление следует подбирать так, чтобы проекция касательной к оптимальной траектории dx/dt на нормаль к поверхности S была бы максимальна:

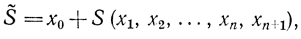
где

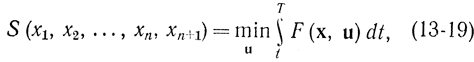
причем следует иметь в виду, эта проекция отрицательна, отсюда ее максимальное значение равно нулю.

Чтобы лучше представить себе поставленный вопрос, рассмотрим частный случай, когда не f_i(i=0,1,...,n,n+1)зависит явно от времени (правые части дифференциальных уравнений и подынтегральная функция функционала не зависят явно от времени) и требуется обеспечить минимальное время переходного процесса Т-t₀. В этом случае F=1, dS/dt=0, нижний предел t=t₀в формуле (13-19) задан.

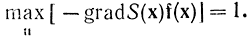
Здесь x и f - n - мерные векторы. Положим

где

получим

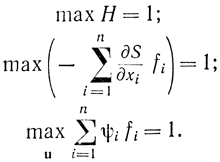
Последние три формулы показывают, что формальные записи принципа максимума и динамического программирования для автономных задач максимального быстродействия совпадают.

В соответствии с формулой (13-21) оптимальное управление следует выбирать так, чтобы максимизировать Н и чтобы скалярное произведение (13-20) было бы равно единице, т. е.

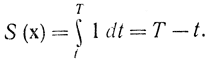
В соответствии с этой формулой поверхность S=const есть поверхность изохрон Т-t=const, причем, величина S убывает по мере приближения к конечной точке. Поэтому вектор ψ, обратный направлению возрастания S (градиенту), направляется внутрь изоповерхности S=const (рис. 13-4).

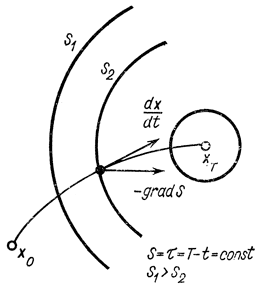
Рис. 13-4. Геометрическая интерпретация динамического программирования

Принцип максимума очевиден и из физических соображений: движение вдоль нормали - самое быстрое по времени, так как движение вдоль поверхности τ=Т-t не дает приближения к конечной точке.

Пример 13-2. Рассмотрим известную нам задачу

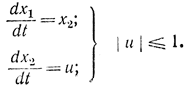
Найдем максимальное быстродействие при начальных (x₁₀, x₂₀) и конечных (x_1T=0, x_2T=0) условиях. Дифференциальное уравнение Беллмана в этом случае запишем как

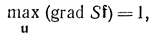
а с учетом того, что шах [-μ]=-minμ,

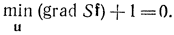
Применив это соотношение к заданной системе, получим:

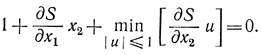
Из этого уравнения следует, что закон оптимального уравнения будет иметь вид:

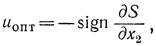
следовательно, u_опт=1 или u_опт=-1. Для определения моментов переключения необходимо решить нелинейное дифференциальное уравнение в частных производных:

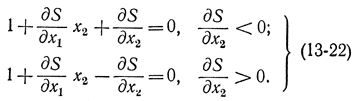
В нашем частном случае это уравнение решается, и мы его решили другим способом (§ 12-4). В соответствии с ним линия переключения задается равенством

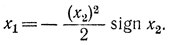
Решением уравнения (13-22) запишется в виде

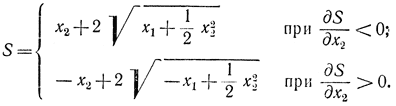
Нетрудно убедится, что оптимальное уравнение

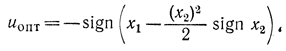
Эта же формула использовалась при синтезе оптимальной системы с помощью фазового пространства.

Покажем на этом примере, что на линии переключения функция Беллмана S разрывна, а скалярное произведение grad Sf непрерывно. На рис. 13-5 показан фазовый портрет для данной задачи, из которого видно, что функция S при переходе точки х (x₁,) сверху вниз через линию переключения скачком меняет свое значение S=х₂ на S=-х₂. Величина скачка уменьшается с приближением к началу координат, так как х₀→0, и в начале координат линия переключения, состоящая из двух кусков парабол, непрерывна. Таким образом, производная от функции S на линии переключения не существует, она терпит бесконечный скачок, хотя следует заметить, что в правой полуплоскости эта функция непрерывная при приближении снизу к линии переключения, а в левой полуплоскости - при приближении сверху. Однако скалярное произведение grad Sf непрерывно при переходе через линию переключения в силу того, что для оптимального управления всегда

Действительно, рассмотрим точку на нижней ветви линии переключения и подсчитаем скалярное произведение при движении сверху и снизу к этой точке. В первом случае имеем:

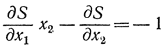
или

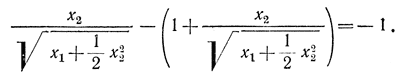
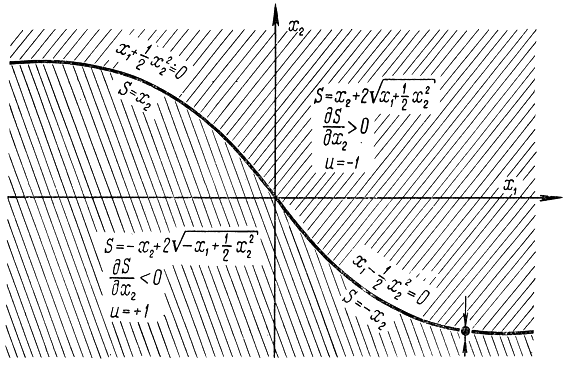
Рис. 13-5. Пояснение к примеру 13-2

Таким образом, при движении сверху скалярное произведение непрерывно. Исследуем движение снизу:

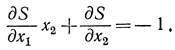
Выполняя дифференцирование, получаем:

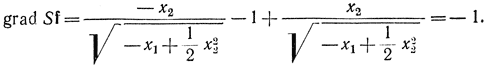
Первый и второй члены этого выражения стремятся при приближении к линии переключения к +∞ и -∞ соответственно, но их разность стремится к нулю.