14-1. Дискретное динамическое программирование как численный метод решения непрерывных задач оптимизации

Существуют два способа численного решения дифференциальных уравнений (в частности, уравнения Беллмана). В первом случае аппроксимируют точное дифференциальное уравнение, например, разностным уравнением, во втором случае представляют непрерывные решения дискретными точками и составляют точное (разностное) уравнение для дискретного процесса. Первый способ, в частности, применяется в численных методах для решения уравнений Эйлера и Понтрягина, второй типичен для динамического программирования и составляет его сущность. В принципе для динамического программирования не требуется составлять дифференциальное уравнение Беллмана. Непрерывная задача оптимального управления решается разбиением непрерывного процесса управления на дискретные этапы, т. е. вместо непрерывного рассматривают поэтапное управление путем поэтапного решения соответствующего функционального уравнения. На каждом этапе, начиная с конца, делают перебор оптимальных управлений из класса допустимых, т. е. удовлетворяющих ограничениям, и выбирают оптимальное, при этом необходимо учитывать, что исходный непрерывный процесс управления должен допускать разбиение на этапы, для которых был бы применим принцип оптимальности Беллмана.

Очевидно, если можно написать критерий оптимальности в виде интегрального функционала, то принцип оптимальности всегда применим в силу аддитивности функционала. Но дискретные процессы управления в принципе могут быть и такими, для которых критерий оптимальности нельзя представить в виде функционала, и тогда вопрос о справедливости принципа оптимальности требует специального рассмотрения. Например, управление на каком-то этапе зависит от управления на n предыдущих этапах. В этом случае выполнения принципа оптимальности можно добиться увеличением размерности фазового пространства (добавлением координат). В теоретической механике этот вопрос, по-видимому, тесно связан с выбором числа независимых координат, т. е. если число координат выбрано малым, то принцип оптимальности неприменим. Но теоретическая механика располагает методами, позволяющими определять минимальное число независимых координат в системе. Как только они выбраны, составляется функция Лагранжа, функционал действия, и тем самым обеспечивается выполнение принципа оптимальности.

Рассмотрим общий путь решения непрерывной вариационной задачи методом дискретного динамического программирования. Пусть требуется определить оптимальное управление, которое минимизирует функционал

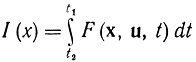
при условии

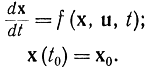
Для этого заменим интеграл суммой, а дифференциальные уравнения разностными:

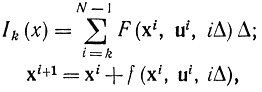
где

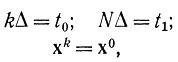
и обозначим

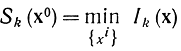
(в этой формуле минимум берется по всем интервалам длины Δ). Применив принцип оптимальности, придем к соотношению

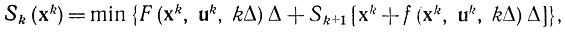
которое позволяет на каждом k-м этапе выбирать оптимальное управление, начиная с последнего (N-1)-го этапа. После того как, начиная с конца, на каждом участке

выбрано оптимальное управление, необходимо двигаться от начала в конец и получить непрерывную траекторию, состоящую из оптимальных кусков и соединяющую начальную и конечную точки.