14-2. Задача о кратчайшем пути

Определим кратчайший путь между пунктами А и В, соединенными сложной сетью дорог (рис. 14-1). Вдоль каждого участка дороги проставлено время движения с учетом покрытия дороги и рельефа местности. Для решения задачи разобьем все расстояние между А и В на этапы. Выбор оптимального пути начнем с конца. Найдем кратчайшие пути, соединяющие пункт В с каждой точкой пересечения линии N-1. Таких оптимальных на последнем участке путей три, они отмечены точками снизу. Затем перейдем к следующему от конца участку, ограниченному прямыми N-2 и N-1. Отметив точки пересечения дорог с прямой N-2 треугольниками, найдем такие пути, соединяющие эти точки с точками пересечения на прямой N-1, которые дадут минимальный суммарный путь на участках (N-2, N-1) и (N-1, N). Эти оптимальные пути отмечены точками сверху.

Естественно, что в качестве второй части пути рассматриваются только оптимальные пути, найденные на последнем участке.

Здесь по существу для следующего от начала участка используется функциональное уравнение

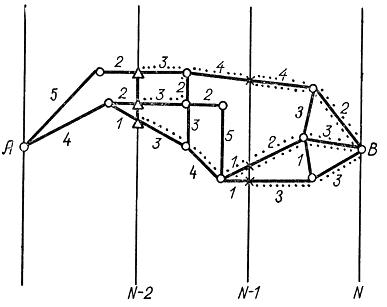
Рис. 14-1. К задаче о кратчайшем пути

После N-2 переходим к первому этапу (см. рис. 14-1), который содержит начальный пункт А. Для этого этапа необходимо соединить А с точками пересечения дорог с прямой N-2 и выбрать оптимальный путь от каждой из этих точек. Затем, делая перебор по этим оптимальным путям и оптимальным путям, соединяющим точки пересечения на прямой N - 2 с точкой В, а затем сравнивая суммарное время движения по ним до точки А, выбираем наилучший. Таким будет путь, время движения по которому равно 18, соединяющий А и В и проходящий через нижнюю точку пересечения прямой N-2 и среднюю точку пересечения N-1, причем перебираются не все пути, соединяющие точки пересечения на прямой N-2 с точкой В, а только оптимальные, уже отобранные на предыдущем этапе расчета. В этом заключается выигрыш, который дает динамическое программирование. Естественно, что реально этапов N может быть несколько сотен и даже тысяч. Может быть несколько путей с оптимальным (одинаковым) временем.

В результате видим, что существенное влияние на успех решения оказывает выбор длины этапа: если ее выбрать такой малой, что точки пересечения на двух соседних прямых соединятся одним путем, то никакого выигрыша метод динамического программирования как метод поэтапного перебора не даст по сравнению с прямым перебором; если ее выбрать слишком большой, то очень много путей соединят каждую пару точек пересечения и эти пути придется долго перебирать. Точных рекомендаций для выбора длины этапа нет. Можно только рекомендовать, чтобы путей, соединяющих две точки пересечения, было не менее 3-5, но не более 8-10. Тогда поэтапный перебор будет проще прямого.

Заметим, что на каждом этапе необходимо выполнить по два перебора:

1. для нахождения минимального пути, соединяющего две точки пересечения (пере-бор всех путей, их соединяющих);
2. для нахождения минимального суммарного пути, состоящего из оптимальных путей, соединяющих точки пересечения левой и правой прямых данного интервала, и оптимальных путей, соединяющих правые точки пересечения с конечной.

Большинство непрерывных задач оптимизации допускает интерпретацию в виде модели, представленной на рис. 14-2. В я-мерном фазовом пространстве (для простоты считаем n - 2) заданы две точки: начальная х₀ и конечная х_T. Требуется соединить их кривой, оптимальной в заданном смысле. Дискретной сети дорог нет, но, по существу, задача допускает интерпретацию, аналогичную задаче с дорогами. На возможные пути наложены некоторые ограничения, например по углу наклона траектории, идущей из заданной точки. Допустим, разрешается двигаться под углом, не выходящим из интервала ±45° к горизонтальному направлению. Этот диапазон квантуют, т. е. разрешается двигаться не в любом, а в одном из 5-10 дискретных направлений внутри допустимого диапазона. Очевидно, что данная задача может решаться методом динамического программирования, так же как и в предыдущем случае.

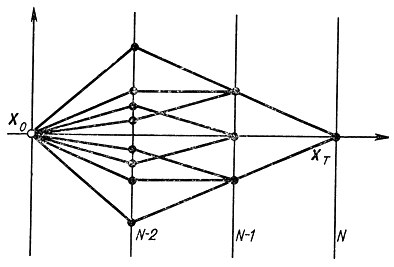
Рис. 14-2. Сведение непрерывных задач к дискретному динамическому программированию