14-3. Задача о критическом пути

Эта задача ставится следующим образом. Задается граф, называемый транспортной сетью, каждой дуге которого x_i, x_j (или х, y) соответствует некоторая величина - длина дуги a(x_i, x_j)≥ 0. Требуется найти кратчайший путь из истока х₀ в сток z. В качестве длины пути Могут фигурировать длина дороги, количество бензина, расходуемое при движении по данному участку, стоимость проезда по данному участку и т. п.

Задача определения критического пути часто возникает в сетевом планировании и управлении. Любая сложная комплексная работа изображается в виде кибернетической модели - сетевого графика, который представляет собой некоторую транспортную сеть. Начальная точка х₀ этой сети соответствует началу, конечная точка z - окончанию комплексных работ (рис. 14-3). Каждая отдельная (частная) работа комплекса показана на рисунке в виде дуги, начальная вершина которой соответствует началу работы, а конечная вершина - концу. Каждой дуге (x_i, x_j) соответствует время выполнения работы t_ij, каждой вершине х_i - время наступления данного события t_i [начала работы, изображенной дугой (x_i, x_j)]. На рис. 14-3 показан сетевой график, состоящий из восьми работ. Если комплекс работ состоит в постройке жилого дома, то отдельными работами могут быть рытье котлована, возведение фундамента, подводка коммуникаций, кладка, штукатурка, вдоль которого суммарное время Рис. 14-3. Пример сетевого графика. выполнения работ было бы максимальным. Он называется критическим. Без его уменьшения невозможно сократить общее время выполнения работ. Критических путей может быть несколько. Тогда для сокращения времени выполнения комплекса работ необходимо уменьшить время выполнения работ, входящих в критические пути. Если ввести в рассмотрение еще и стоимости выполнения работ, то в данном критическом пути следует сокращать те работы, которые обладают наименьшим увеличением стоимости при сокращении времени выполнения работ, т. е. если обозначить зависимость стоимости выполнения работы от времени через c_ij=f_ij(t_ij) то сокращать следует ту работу критического пути, для которой производная

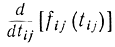
будет максимальной. После сокращения времени одного критического пути может появиться другой критический путь.

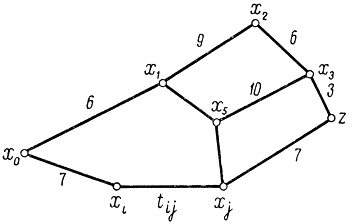
Рис. 14-3. Пример сетевого графика

Известно много алгоритмов для отыскания критического пути в сетевом графике. Здесь будет рассмотрен только алгоритм Беллмана - Калаба [Л. 90]. Он основан на принципе оптимальности и использует функциональное уравнение Беллмана. Принцип оптимальности Беллмана в данном случае можно сформулировать так: любой максимальный (критический) путь, содержащий не более r дуг, образован частичными путями, содержащими не более k(k≤r) дуг, которые (пути) также максимальны.

Для всякой дуги, не принадлежащей нашей сети, т. е. (x_i, x_j)∈U, положим t_ij=-∞ и t_ii= 0. Тогда задача будет состоять в отыскании пути

для которого сумма

достигает максимума. Здесь - события, соответствующие вершинам сети (моментам начала и окончания работ); t_ij- время выполнения работы, которая начинается событием E_i и заканчивается событием E_j. Составим функциональное уравнение Беллмана:

где величины v_i(i=1, 2,..., n-1) являются критическими временами частичных путей от i-й до конечной вершины. Вычисления начнем с конца, полагая

Далее, на втором шаге

Величина v¹_i содержит значения времени выполнения операций на путях, состоящих из одной дуги, которые заканчиваются в конечной вершине. Соотношения (14-1) позволяют выбрать максимальный путь, состоящий из двух дуг (которые заканчиваются в конечной точке). Дальнейшие вычисления выполним в соответствии с рекуррентной формулой

Вычисления будут закончены, когда

Величины v^k_i составляют времена отдельных критических путей, входящих в общее время t_kp критического пути.

Можно показать, что требуется всего n-2 итераций вида (14-2), где n - число вершин сети. Величины v^k_i являются значениями функции Беллмана S для k-го этапа.

Пример 14-1. Найдем критический путь в сети, показанной на рис. 14-4. Этой сети соответствует матрица, каждый элемент которой a_ij равен времени выполнения операции t_ij. Там, где ребра отсутствуют, поставлена ∞. С помощью формулы (14-2) составим таблицу значений v^k_i (табл. 14-1):

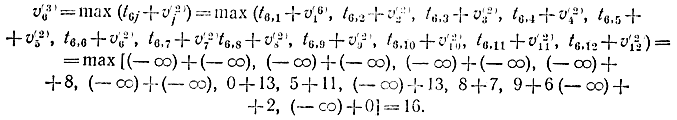
На рис. 14-4 в кружках отмечены максимальные значения путей, ведущих из i-й вершины в конечную точку ( 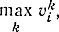т.е. по числу дуг). Критический путь отмечен двойной линией, время критического пути t_kp=33

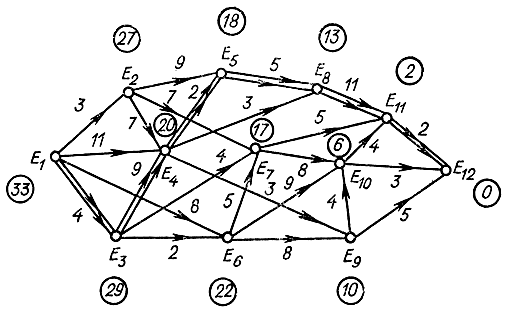
Рис. 14-4. Сетевой график для примера 14-1

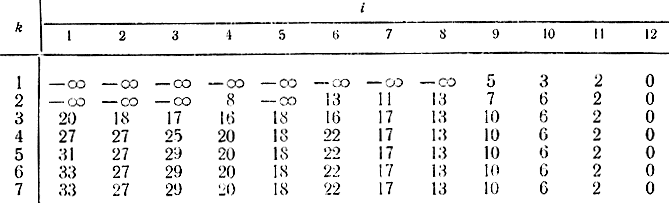
Таблица 14-1