14-4. Задача распределения ресурсов

Рассмотрим типичную для динамического программирования задачу распределения ресурсов. Допустим, имеется в наличии у средств и четыре отрасли, в которые эти средства необходимо вложить оптимальным образом. Аналитически, графически или в виде таблиц должны быть заданы функции прибыли g₁(y)/g₄(y) в зависимости от вложений в каждую отрасль. Зададим их с помощью табл. 14-2.

Таблица 14-2

Требуется оптимальным способом распределить исходные средства, т. е. чтобы суммарный доход

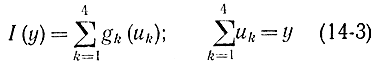
был максимален. Для простоты предположим, что средства представлены целыми единицами (миллионами рублей). Это условие не является принципиальным для данной задачи и не означает, что задача становится целочисленной (см. гл. 18). Обозначим оптимальную прибыль при суммарном вложении у по одной отрасли через Φ₁(y)=S₁(y), по двум - Φ₁₂(y)=S₂(y), по трем - Φ₁₂₃(y)=S₃(y), по четырем -Φ₁₂₃₄(y)=S₄(y). Это и будут функции Беллмана для разных этапов. Оказывается, распределение ресурсов как процесс определения оптимального управления тоже можно разделить на этапы, хотя здесь нет никакого физического процесса во времени. Условно вводится первый этап, называемый иногда нулевым, на котором все средства вкладываются в одну отрасль, например в первую. На втором этапе выбирается оптимальное распределение между двумя любыми отраслями, например между первой и второй, причем, так как результаты оптимального перебора на первом этапе согласно функциональному уравнению Беллмана будут использоваться на последующих этапах, то оптимальный перебор на втором этапе следует делать для разных значений исходного капитала y. В результате прохождения второго этапа составляется табл. 14-3 оптимальных распределений между первой и второй отраслями.

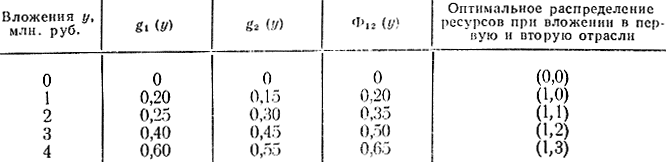
Таблица 14-3

Для определения необходимых прибылей используется таблица или соответствующие графики (рис. 14-4). После составления табл. 14-3 переходят к третьему этапу и определяют оптимальное распределение между первой, второй и третьей отраслями, используя результаты первого этапа. При этом составляется табл. 14-4 оптимальных распределений для разных значений исходного капитала. Наконец, переходят к последнему, четвертому этапу и составляют табл. 14-5 оптимальных распределений по четырем отраслям.

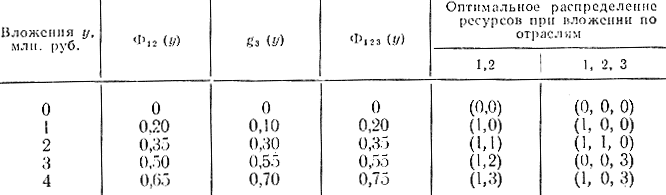
Таблица 14-4

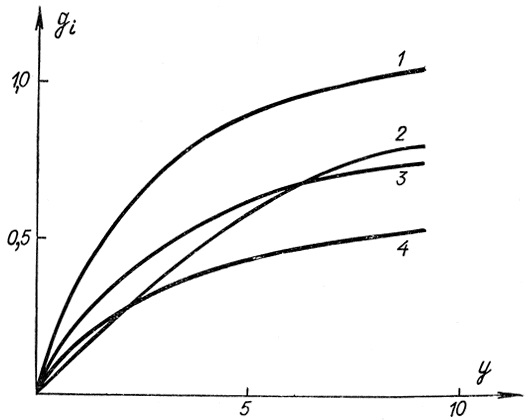
Рис. 14-5. К задаче распределения ресурсов

Для составления таблиц использовались следующие формулы:

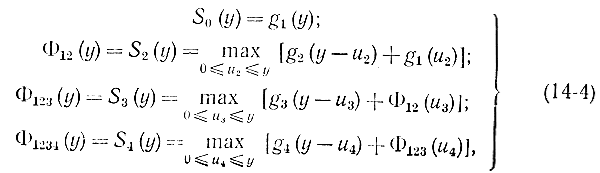
Таблица 14-5

каждая из которых представляет собой функциональное уравнение Беллмана, которое в общем случае для k отраслей запишется в виде

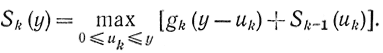
Для определения оптимальной политики на каждом этапе приходится комбинировать значения из третьего столбца со значением из второго столбца и определять максимальную сумму в каждой таблице. Так, для определения оптимальной политики на третьем этапе при вложении y=3 необходимо при прямом переборе сравнить следующие семь политик: (3, 0, 0), (2, 1, 0), (1, 1, 1), (0, 2, 1), (0, 1, 2), (0, 0, 3), (0, 1, 2). Однако этот перебор можно сократить, используя соотношение (14-4), т. е. достаточно вычислить значения двух функций S₂ и g₃ для четырех значений u₃ (табл. 14-6).

Таблица 14-6

Из табл. 14-6 следует, что наилучшей политикой на третьем этапе будет u₃=3 и S₂(0). С помощью последнего столбца табл. 14-4 или 14-3 получим для S₂(0) u₁=0, u₂=0. Поэтому окончательно оптимальной политикой на третьем этапе при y=3 будет (0, 0, 3), что и занесено в последний столбец табл. 14-4.

Таким образом, благодаря принципу оптимальности и функциональному уравнению Беллмана вместо сравнения суммарных доходов восьми вариантов распределения потребовалось сравнение только четырех вариантов (табл. 14-6).

Для сравнения в табл. 14-4 и 14-5 в предпоследних столбцах приведены оптимальные стратегии предыдущих этапов.

Благодаря такому поэтапному перебору существенно сокращается трудоемкость. Если же распределять средства сразу между четырьмя отраслями:

(5, 0, 0, 0), (4, 1, 0, 0), (4, 0, 1,0), (4, 0, 0, 1), (3, 1, 1, 0), (3 0, 1, 1), (3,2, 0,0), (3,0, 2,0), (3,0, 0, 2), (2, 1,1,1), (2, 2 0, 1), (2, 2, 1, 0), (2, 0, 2, 1) и т. д., то возникает необходимость перебора большого количества вариантов.

С увеличением числа ассигнований и отраслей объем перебора интенсивно возрастает. Так, для =k4 при y≥10 число вариантов составит 286, при у 10 это число равно 1 001. Для k числа отраслей процесс оптимального распределения ресурсов распадается на k=1 этапов.

На примере задачи распределения ресурсов продемонстрирована модификация метода динамического программирования для процессов, не развивающихся во времени. Процесс искусственно разворачивается во времени. В этом смысл динамического программирования как оптимального метода перебора, как метода решения комбинаторных задач перебора.

Заметим, что в этой задаче требуется вычислить значения функции Беллмана S_k=1 на (k-1)-м шаге для всех значений аргумента, так как для решения функционального уравнения на k-м шаге требуется перебрать все допустимые значения этой функции. Соответственно на каждом шаге, как правило, вычисляется полная таблица значений функции Беллмана. Пошаговая процедура вычислений в данной задаче оказалась возможной благодаря зависимости дохода в каждой отрасли только от вложения в данную отрасль и независимости от вклада в другие отрасли, взятые по отдельности и в сумме. Это свойство обеспечило выполнение принципа оптимальности Беллмана для дискретных много шаговых процессов.