14-5. Транспортная задача

Можно дать следующую формулировку транспортной задачи. Имеются m складов ресурсов и n пунктов потребления (m истоков и n стоков). Для простоты рассмотрим случай с одним ресурсом. Обозначим через a_i- запасы ресурсов на i-м складе (i = 1,2,...,m), b_j количество ресурсов, ожидаемое в j-м пункте потребления (j= 1,2, ..., n). Предполагается, что суммарный запас равен суммарному спросу:

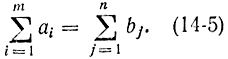
Задачу можно решать и без этого ограничения, считая, что суммарные запасы превышают суммарные запросы. Однако для простоты дадим решение при условии (14-5). Через x_ij обозначим количество ресурсов, перевозимое с i-го склада на j-й пункт потребления. Стоимость такой перевозки определяется функцией g_ij(x_ij), которая может задаваться аналитически, графически или с помощью таблиц. Считается, что нельзя перевозить ресурсы через перевалочные пункты, т. е. справедливы следующие условия:

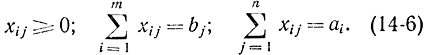
В этой задаче требуется определить величины x_ij, удовлетворяющие условиям (14-6), при которых суммарная стоимость перевозок будет минимальна, т. е.

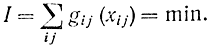
Часто функции стоимости перевозок являются линейными функциями величин x_ij:

Транспортная задача в общем случае - это задача нелинейного программирования, где в качестве ограничений выступают соотношения (14-6). При условии (14-7) она становится задачей линейного программирования и может быть решена симплекс-методом, рассмотренным в гл. 16.

Для простоты ограничимся вариантом с двумя складами m=2 и несколькими пунктами потребления n. Решение задачи для более сложных случаев (m>2) сталкивается с большими вычислительными трудностями, известными под названием "проклятие размерности", преодолеть которые полностью на сегодняшний день не удается, и излагается в специальной литературе по динамическому программированию [Л.80]. Для решения задачи при m=2 прежде всего представим статический процесс перевозки как динамический в виде последовательности этапов. В качестве первого этапа выберем удовлетворение спроса n-го пункта потребления, затем перейдем к (n-1)-у и т. д. Составим для такого поэтапного процесса функциональное уравнение Беллмана. Введем функцию S_k(a₁, a₂), k= 1, 2, ..., n как величину затрат при использовании оптимальной политики, когда начинают с количества a₁ и a₂ ресурсов на складах при потребностях b_j(j=1, 2, ..., n) в пунктах потребления.

На первом этапе (k=1) удовлетворяются потребности j-го пункта потребления; при этом получаются затраты

Запасы ресурсов на складах уменьшаются соответственно до a₁-x_1n и a₂-x_2n поэтому

при условиях, что

На втором этапе удовлетворяются потребности n-го и (n-1)-го пунктов потребления. Для этого используется рекуррентное соотношение Беллмана (функциональное уравнение):

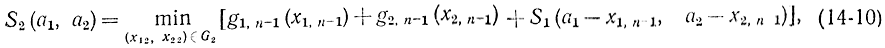
где область G₂ определяется соотношениями

Запись (14-10) означает оптимальное обеспечение (по расходам на перевозки) потребностей (n-1)-го пункта потребления при том условии, что они удовлетворены для n-го пункта потребления. Выполнение этого условия обеспечивается самим определением функции Sx в соответствии с формулами (14-8) и (14-9), в частности, первое из условий (14-9) означает полное удовлетворение спроса n-го пункта потребления. Очевидно, что n-й номер можно поменять на первый, изменив нумерацию или определив первый этап как удовлетворение потребностей первого пункта, отчего оптимальность значений не изменится. Последовательность выполнения операций "с конца" характерна для динамического программирования и обусловливается принципом оптимальности.

Из соотношения (14-10), так же как в задаче о распределении ресурсов, следует, что на каждом этапе необходимо иметь значения функции Беллмана для всех значений аргумента, чтобы выбрать из них наилучшее при составлении функционального уравнения Беллмана для последующего этапа. Последнее соотношение (14-9) искусственно вводится для полноты рекуррентного процесса вычислений.

Пошаговый процесс оптимизации оказался возможным благодаря зависимости стоимости перевозки с i-го склада к j-у потребителю только от величины груза, перевозимого между этими пунктами, и ее независимости от величины груза, перевозимого с других складов к этому же j-у потребителю и со всех складов (включая i-й) к другим потребителям. Это обеспечило выполнение принципа оптимальности Беллмана для данной задачи.

Для любого k≥1 получаем:

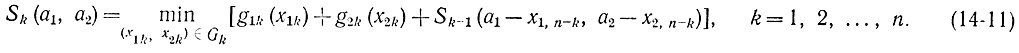
Минимизация в этой формуле производится по обеим переменным x_1k, x_2k из области G, которая определяется условиями

Если заменить

то уравнение (14-11) запишется в стандартном для динамического программирования виде:

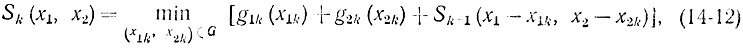
где

Уравнение (14-12) аналогично ранее рассмотренным функциональным уравнениям в задаче о распределении ресурсов за исключением двух моментов. Во-первых, на переменные, по которым ищется экстремум, наложено больше ограничений, т. е. это - вариационная задача с ограничениями. Как уже указывалось, такие задачи трудно решать методами классического вариационного исчисления из-за недифференцируемости функций на границе области допустимых изменений переменных. Метод динамического программирования практически снимает трудности с введением ограничений, необходимо лишь на каждом этапе проверять пределы допустимой области. Во-вторых, транспортная задача с двумя складами является двумерной задачей динамического программирования, так как функция Беллмана зависит от двух переменных, тогда как предыдущие задачи (о распределении ресурсов, о критическом пути и т. д.) были одномерными: оптимальным образом распределялся один капитал или выбиралось только время движения (а не время и стоимость). Задача о распределении ресурсов становится многомерной, если между отраслями необходимо оптимальным образом распределить несколько видов ресурсов: капитал, рабочую силу, технику. Объем вычислений по методу динамического программирования интенсивно увеличивается с возрастанием размерности задачи, особенно в части объема требуемой памяти машины. Это составляет один из существенных недостатков динамического программирования, который Беллман называет "проклятием размерности".

Двумерную транспортную задачу легко свести к одномерной, если использовать соотношение (14-4), которое для двух складов (m= 2) запишется в виде

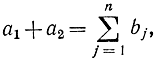
или в других обозначениях [см. формулу (14-12)]

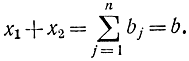
Из последнего уравнения при заданном суммарном спросе всегда величину х₂ можно выразить через x₁ поэтому

Отсюда соотношение (14-12) перепишется в виде

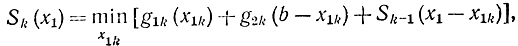
где величина x_1k подчиняется условиям

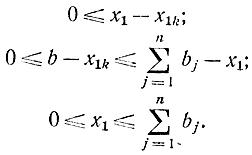
Благодаря этому приему общая задача с m складами может быть сведена к задаче с m-1 складом, т. е. m-мерная задача сведется к (m-1)- мерной, в результате чего ее размерность понизится на единицу.

Пример 14-2. Рассмотрим числовой пример решения транспортной задачи с помощью динамического программирования для случая с двумя складами и восемью пунктами потребления, т. е. т- 2 и п = 8. Функцию стоимости возьмем в виде

Таким образом, стоимость перевозки из одного пункта в другой представляет собой квадратичную функцию перевозимого количества, где свободный член - сумма двух величин, зависящих от перевозимого количества. Первое слагаемое характеризует организационные расходы и определяется следующим образом:

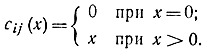
Второе слагаемое характеризует штраф за недостаточно полное использование транспортной линии и определяется соотношением

Соответствующие значения коэффициентов приведены в табл. 14-7.

Так, стоимость перевозки из первого склада к седьмому потребителю задается формулой

Получим оптимальное решение задачи методом динамического программирования при начальных запасах на складах а₁=40, а₂=50. Результаты решения сведены в табл. 14-8.

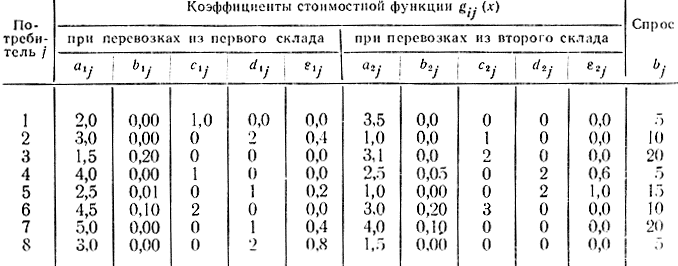
Таблица 14-7

Полная стоимость перевозок равна С=274,6864. Расчеты производились на ЦВМ М-20 с шагом 0,2 изменения переменных управления.

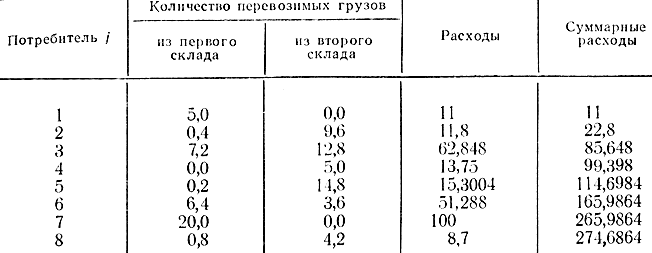
Таблица 14-8

Ниже будет дано решение транспортной задачи методом дискретного принципа максимума Понтрягина и сравнение этих двух методов.