14-6. Блок-схема вычислительного процесса для динамического программирования

На рис. 14-6 представлена блок-схема вычислительного процесса для решения задачи распределения ресурсов методом динамического программирования. Она может служить основой для составления программы любой задачи, решаемой на ЦВМ методом дискретного динамического программирования. Имеются в виду задачи о распределении ресурсов, транспортная и другие, для которых удается составить модель динамического поэтапного процесса.

Дадим пояснения к блок-схеме на рис. 14-6. Основная часть схемы реализует рекуррентное соотношение Беллмана, согласно которому из функции S_k-1 получается функция S_k. Однако в блок-схеме, особенно вначале, имеются специальные блоки, позволяющие вычислять Sx в плане общей процедуры в соответствии с уравнением

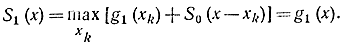
Для этого предполагаем, что S₀(x)=0 (блок 1). Индекс k, обозначающий число способов распределения, вначале принимает значение k=1 (блок 2). Блок 3 вычисляет значение S₁(х)=g₁(х) для x=0, Δ, 2Δ... Символ β, которому отводится определенная ячейка памяти, условно означает "лучший доход до сих пор" и предназначается для того, чтобы реализовать операцию максимизации. Процесс максимизации начинают записью в память максимального по модулю отрицательного числа, условно обозначаемого - ∞(блок 4), процесс минимизации - записью максимального по модулю положительного числа, условно обозначаемого +∞. Это тоже условный прием, имеющий целью исключить начало процесса решения, как особый случай. В блоке 5 в блок-схему вводится обозначение (присваивается наименование, код) x_k(x) для оптимального распределения на k-м шаге. На начальном Шаге k=1, х=0 и нулевое значение испытывается в качестве начального значения для x₁(0). В блоке 6 вычисляется очередное значение суммы

которое обозначается через α и засылается в определенную ячейку памяти.

Блок 7 сравнивает текущее значение дохода α с "лучшим доходом до сих пор" β если α больше β, то блок 2 заменяет α→β, новому значению х_k(x) присваивается смысл "наилучшего до сих пор значения ресурса" с отведением ячейки памяти γ,и через блок 9 осуществляется переход от x_k(x) к x_k(k)+Δ если α меньше β, замены α→β не происходит, в памяти сохраняется прежнее β, значение а забывается и через блок 9 делается очередная замена x_k(x)+Δ→x_k(x). Для процесса минимизации знаки неравенств следует поменять на обратные. Если новое значение x_k(x)+Δ больше общего количества выделяемых ресурсов x (блок 10), то оно не рассматривается и осуществляется переход к блоку 11; если значение x_k(x)+Δ допустимо, то оно поступает на блок 6 для повторения процесса. В блоке 11 происходит запоминание полученных оптимальных значений x_k(х) и S_k(х) (им в памяти присваиваются наименования γ и β соответственно). В блоке 12 общее число ресурсов увеличивается на шаг: x+Δ заменяет х. Блок 13 проверяет, не превышает ли новое значение ресурсов их общего предельного значения х_макс. Если значение x+Δ больше x_макс полученные данные x_k(х) и S_k(x) выдаются в магнитную память пли на печать (блок 14). Блок 15 предназначен для замены старых массивов S_k-1(х) на новые S_k(х), которые будут использоваться в процессе сравнения на следующем шаге с S_k+1(х). Блок 16 означает переход от k-го этапа к (k+1)-му этапу, т. е. вместо к процессов (по две, по три отрасли и т. д.) рассматриваются k+1.

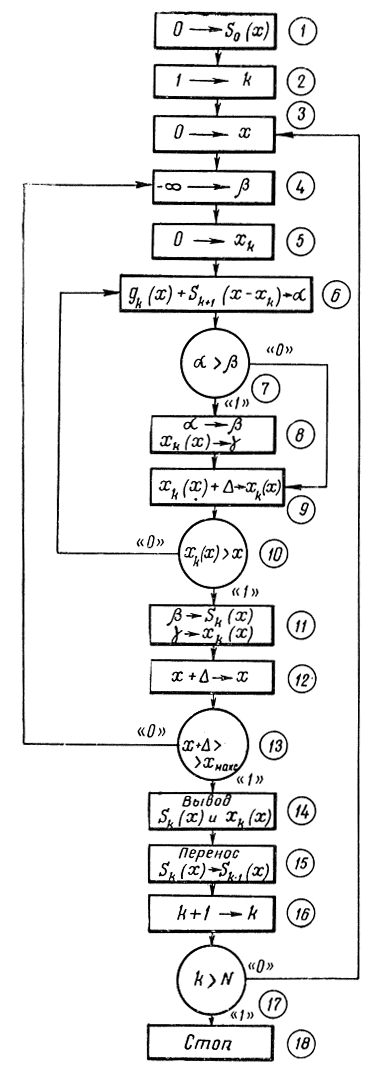
Рис. 14-6. Блок-схема вычислительного процесса для динамического программирования

Блок 17 проверяет, не исчерпаны ли все возможные количества процессов N. Если ответ отрицательный, то с блока 3 начинается процесс вычислений с увеличенным на единицу к. Если k+1>N, процесс заканчивается (блок 18) и на печать выдается результат с выхода блока 14.