14-7. Формальный математический аппарат

Здесь приводится общий математический аппарат, рассмотренный ранее на отдельных частных примерах, и выводится функциональное уравнение Беллмана. Так же как и в непрерывном случае, оно справедливо при выполнении принципа оптимальности, который аналогичен принципу оптимальности в непрерывном случае, но имеет свои особенности.

Предположим, что при распределении х средств между N отраслями необходимо добиться максимального дохода I(x₁, x₂,...,x_N). Считается, что

Ресурсы x_i имеют общую меру и удовлетворяют условию

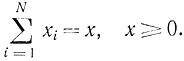
Такие нелинейные функции носят название сепарабельных. Они типичны для динамического программирования и будут встречаться и дальше. Для таких функций можно построить динамический процесс, для которого заведомо справедлив принцип оптимальности Беллмана, аналогично тому, как это было сделано в задаче о распределении ресурсов.

Требуется найти

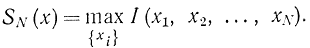
Функция (14-14) обладает свойством аддитивности доходов по всем отраслям. Оно обеспечивает выполнение принципа оптимальности Беллмана, который для дискретных процессов управления может быть сформулирован следующим образом: последующие решения должны составлять оптимальное поведение относительно предыдущего состояния, полученного в результате решения на предыдущем этапе, независимо от того, какими бы эти состояние и решение ни были. Дискретное динамическое программирование применимо только к таким много шаговым процессам управления. Для функции (14-14) этот принцип заведомо выполнен, так как доход от вложения ресурсов в данную отрасль зависит только от количества ресурсов, вложенных в эту отрасль, и не зависит от количества ресурсов, вложенных в другие отрасли. Именно это обстоятельство позволяет построить много шаговый процесс типа "первый шаг - вклад в первую отрасль, второй шаг - вклад в первые две отрасли и т. д.", для которого справедлив принцип оптимальности. Иначе смысл принципа оптимальности можно сформулировать так: много шаговый процесс удовлетворяет принципу оптимальности Беллмана, если функция цели, принимающая на k-м шаге оптимальное значение при х=x^k, принимает, также оптимальное значение для оставшихся k=1 шагов при том же х=x^k. Если функция суммарного дохода является не сепарабельной, то нельзя построить много шаговый процесс, для которого удовлетворяется принцип оптимальности.

Имеется много приемов преобразования исходной задачи для удовлетворения принципа оптимальности, которые в основном разделяются на две группы. В первом случае сводят не сепарабельную функцию цели к сепарабельной. Во втором случае преобразуют уже сам много шаговый процесс. В обоих случаях для удовлетворения принципа оптимальности приходится усложнять задачу введением дополнительных ограничений на область изменения переменных, что не очень сильно усложняет вычислительную процедуру, или введением дополнительных переменных, что фактически приводит к увеличению размерности решаемой задачи и к практически не реализуемым по сложности вычислительным процедурам. Поэтому во многих случаях этот второй прием вряд ли можно расценивать как решение задачи. В качестве примера рассмотрим два варианта сведения функций к сепарабельным. Так, если в функции цели встречаются слагаемые вида x_ix_j, то введением двух новых переменных

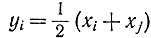
и

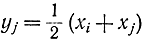
можно преобразовать их к сепарабельной форме

Сепарабельная форма здесь достигается введением новых переменных, не увеличивающих размерность задачи (увеличивается число отраслей), и добавлением ограничений по два на каждый член вида x_ix_j.

Если в функции цели I встречаются члены вида g_i(x_i,x_i-1), то доход в данной отрасли будет зависеть от величины вложений в эту и соседнюю (i-1)-ю отрасли. Введением дополнительной переменной y_i=x_i-1 получаем для такого случая зависимость функции дохода от двух переменных g_i(x_i, y_i). Здесь возникает трудность, связанная с увеличением размерности задачи, так как функция цели I зависит уже от двух видов ресурсов x_i и y_i которые в данном случае связаны ограничением, а в общем случае двумерной задачи о распределении они могут быть друг от друга независимы. Характерной особенностью много шаговых процессов, которые оптимизируются с помощью динамического программирования, является зависимость текущего состояния только от предыдущего и независимость от состояний, предшествующих этому предыдущему (отсутствие последействия). Только в этом случае удается составить функциональное уравнение Беллмана. Ранее рассмотренный вариант, в котором функция g_i(x_i, x_i-1) зависела от двух переменных без их замены, приводит к много шаговому процессу, не удовлетворяющему этому условию. Однако с помощью только что проделанной замены y_j=x_i-1 - много шаговый процесс становится процессом без последействия.

Если доходы в разных отраслях связаны между собой, то принцип оптимальности Беллмана также несправедлив.

При условии (14-14) функциональное уравнение Беллмана имеет вид:

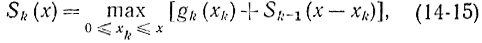
причем x - общее число ресурсов; x_i - количество ресурсов, вкладываемое в i-ю отрасль, причем 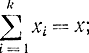g_k(x_k)- доход от вложения x средств в k-ю отрасль (k=1, 2,..., N). Благодаря этому соотношению имеется N этапов, где N - число отраслей. Формально можно получить уравнение (14-15), используя следующее соотношение, основанное на принципе оптимальности:

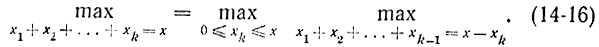
Это равенство означает, что доход в k-и отрасли не зависит от дохода в остальных -k1 отраслях и благодаря этому максимальный доход по всем отраслям равен сумме максимального дохода по всем -k1 отраслям и по k-й отрасли. С помощью формулы (14-16) напишем цепочку равенств:

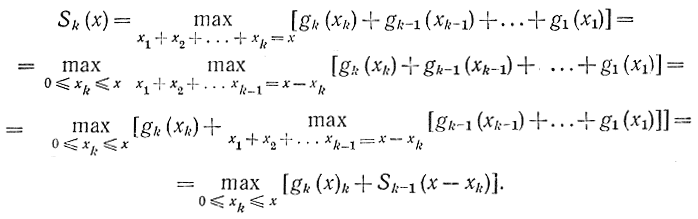
Тем самым получено функциональное уравнение с использованием свойства аддитивности функционала (14-15), обеспечивающего выполнение принципа оптимальности Беллмана. Согласно этому уравнению динамическое программирование заменяет прямой перебор направленным, поэтапным [на каждом k-м шаге используется результат перебора на предыдущем (k-1)-м шаге], который существенно сокращает число вариантов.

Если в задаче распределения имеется несколько видов ресурсов, не имеющих общей меры, то она становится многомерной. Так, в случае с. двумя ресурсами суммарный доход равен:

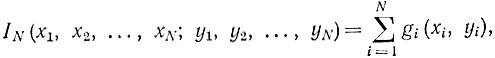
где

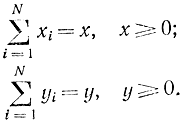
Функция Беллмана определяется как

причем для N=1

для N≥2

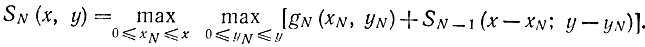
Такой вид имеет функциональное уравнение Беллмана для двумерного случая.