14-8. Эффективность динамического программирования

Постараемся оценить объем направленного перебора при динамическом программировании и сравнить его с прямым перебором. В общей одномерной задаче распределения ресурсов для n отраслей при прямом переборе число вариантов

где m - число дискретных значений, которые могут принимать x_i; n - число переменных (отраслей). Если n=2, m=3, т. е. x₁(a₁, a₂, a₃), x₂(b₁, b₂, b₃), то возможных комбинаций, которые необходимо проверить при прямом переборе, будет a₁b₁, a₁b₂, a₁b₃, a₂b₁, a₂b₂, a₂b₃, a₃b₁, a₃b₂, a₃b₃ - всего 9=3².

Точную формулу для числа перебираемых вариантов при динамическом программировании написать не удается, так как в каждой задаче она своя. Однако можно утверждать, что зависимость числа вариантов от n не экспоненциальная, а примерно линейная.

Для ориентации рассмотрим задачу нелинейного целочисленного программирования в виде

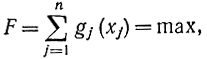
причем 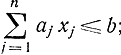; a_j>0; x≥0(x_j- целые числа); j=1,.., n.

Для простоты положим a_j=1. При определении максимума F необходимо вычислить значения f_j(x_j) для каждого из b+1 значений, которые может принимать x_j. Найдем нижнюю границу числа набора целых значений x_j, удовлетворяющих условию

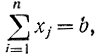
т. е. вместо неравенства рассмотрим строгое равенство. Для случая прямого перебора искомое количество равно числу способов, которыми

можно разместить, например, b одинаковых шаров в n урн. Это число равно числу сочетаний из n+b-1 по b, т. е.

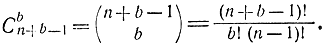
Для N=5 и b=20 получим:

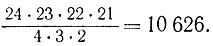
Это означает, что при прямом переборе необходимо вычислить значения F для 10 626 различных комбинаций значений x_i. Теперь оценим объем вычислений при направленном переборе в случае динамического программирования. Для определения значений функции Беллмана S_k(х) при заданном х необходимо выполнить х+1 вычисление. Чтобы построить всю таблицу значений функции S_k(x), необходимо осуществить вычисления в количестве

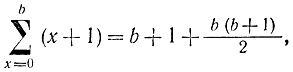
откуда для подсчета всех необходимых значений -k1 функций S_k(х) потребуется

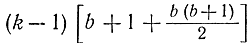
вычислений. Для последней функции S_k требуется найти ее значение S_k(b). Поэтому здесь необходимо вычислить только b+1 значение. Таким образом, общее число вычислений при динамическом программировании определяется формулой

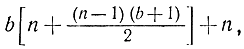
которое при n=5 и b=20 равно 945, что составляет примерно 10% от объема 10 626 вычислений при прямом переборе.

При решении непрерывных задач отыскания экстремума с помощью динамического программирования встает еще проблема интерполяции промежуточных значений функции S_n-1 для подсчета значений S_n в соответствии с функциональным уравнением Беллмана

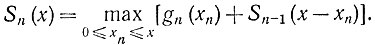
Дело в том, что заготовленная на (n-1)-м шаге таблица дискретных значений функции S_n-1 может не содержать необходимого значения аргумента, при котором функция S_n принимает максимальное значение, так как х и все остальные переменные меняются непрерывно. В этом случае приходится по линейному или другому закону интерполировать промежуточные между двумя табличными значения S_n-1.