14-9. Задачи планирования

В кибернетике большинство задач оптимизации делится на две группы: распределения и расписания. В задачах первой группы (распределения ресурсов, транспортной) время, как правило, отсутствует. В задачах второй группы, которые часто возникают в автоматизированных системах управления, требуется ресурсы распределить по времени. Встречаются и смешанные задачи распределения и расписания, в которых требуется одновременно оптимальным образом распределить ресурсы по объектам и расписать это распределение по времени.

Рассмотрим модель задачи планирования во времени, часто называемую задачей расписания, под которой понимается оптимальное распределение ресурсов во времени. В качестве ресурсов могут выступать финансы, топливо, энергия, работа, приборы, транспортные средства.

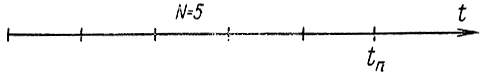
Рис. 14-7. Пояснение к задаче планирования

Считается, что ресурсы могут распределяться только дискретно с шагом, равным единице или Δ. Допустим, что весь временной интервал планирования t_п (рис. 14-7) разделен на N одинаковых интервалов времени. На планирование выделено определенное количество ресурсов х и задана величина доходов (или расходов) g_i(x_i) на каждом интервале от вложения на нем x_i ресурсов; при этом, чтобы был справедлив принцип оптимальности, считаем, что доход на i-м интервале зависит только от количества ресурсов, выделенных на этом интервале, и не зависит от ресурсов, выделенных на предыдущих i-1, i-2 и т. д. интервалах. Требуется оптимальным способом распределить ресурсы х на всем интервале, чтобы суммарный доход был максимален (или расход минимален):

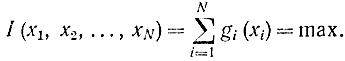
Для построения динамического процесса планирования считаем, что ресурсы вкладываются все на одном интервале, потом - все на двух и т. д. Тогда получаем рекуррентный процесс, аналогичный полученному в задаче распределения по отраслям. Общее рекуррентное соотношение Беллмана будет иметь вид:

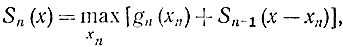
где n=2, 3, 4, ..., N, причем

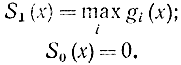
Теперь разберем усложненные варианты рассмотренной задачи.

1. Допустим, что один и тот же вид ресурсов вкладывается на каждом интервале в М отраслей, причем в самом общем случае число M зависит от интервала n, т. е. M=f(n). Для простейшего варианта можно считать, что доход на каждом интервале от вложения в m-ю отрасль зависит только от количества вложенных ресурсов x^m_n и равен g(x^m_n), n=1,2,...,N; m=1,2,...,M. В этом случае общий доход
   
   
   при
   
   
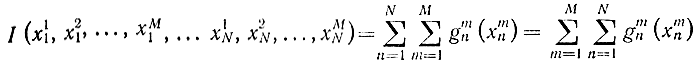   Необходимо, чтобы I достигло максимума. Такая задача решается методом динамического программирования, но вначале необходимо решить классическую задачу распределения ресурсов по отраслям для одного, потом для двух интервалов времени. Или, наоборот, вначале распределить ресурсы для одной отрасли и всех интервалов времени, потом для двух отраслей и всех интервалов и т. д. Здесь уже имеет место смешанная задача распределения (назначения, прикрепления) и расписания. Однако благодаря линейности она сводится к классической задаче о распределении ресурсов в NM отраслей и решается динамическим программированием.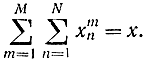
2. Допустим, имеется L разных дискретных ресурсов. Если сохраняется принцип независимости их друг от друга, то принцип оптимальности справедлив и можно решать задачу аналогично предыдущему. Вначале распределить L ресурсов между М отраслями для одного интервала времени, потом для двух, трех и т. д. Функция цели будет иметь вид:
   
   

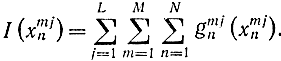
Дальнейшее обобщение задачи заключается в соблюдении заданной последовательности работ, которые в данной модели совпадают с отраслями, а ресурсы включают в себя и рабочую силу. Такая последовательность часто задается в виде сетевого графика и аналитически записывается в виде ограничений. Если еще ввести понятие рабочего места (станка) и условие "привязки" работы к рабочему месту, то получится задача календарного планирования, которая имеет чрезвычайно большое значение для АСУ.