14-10. Стохастические задачи динамического программирования

В планировании и управлении часто присутствует элемент случайности, поэтому задачи, возникающие при планировании в больших системах, состоящих из тысяч и сотен тысяч индивидуальных систем, невозможно решать детерминированным образом и приходится прибегать к укрупнению и вероятностному или стохастическому планированию, одним из способов которого является вероятностное динамическое программирование [Л.86, 92].

Задача с игрушечных дел мастером. Мастер делает в течение недели игрушку одного типа. Если она имеет успех, то на следующей неделе он продолжает ее изготовление, если нет, он переходит к игрушке другого типа. Мастер небогат и подчиняет свою стратегию результатам предыдущей недели. Очевидно, что данный случайный процесс является марковским, так как в нем вероятность перехода в новое состояние зависит только от непосредственно предыдущего (и этого нового) состояния и не зависит от состояний, предшествующих предыдущему.

Рис. 14-8. Интерпретация процесса принятия решений игрушечных дел мастером.

Допустим, в каждый понедельник L_i мастер выбирает модель. Тогда получится бесконечный процесс, изображенный условно на рис. 14-8. В каждом исходе (удачная или неудачная модель) мастер может применить две стратегии: в случае удачной игрушки - использовать или не использовать рекламу, в случае неудачной игрушки - проводить или не проводить исследования. Тогда, с одной стороны, доход g²₂₁ с рекламой в случае, если мастер делает после удачной игрушки опять ее же, будет меньше, чем без рекламы, так как на рекламу затрачены средства (табл. 14-9). Так же и доход в случае с неудачной игрушкой будет еще меньше, если мастер после неудачной i-й игрушки опять пустит ее в производство после исследований, так как часть средств уйдет на исследование.

Но, с другой стороны, вероятность p²₁₁ того, что удачная игрушка с рекламой будет снова удачной, больше, чем без рекламы:

и вероятность появления удачной игрушки после неудачной в результате исследований больше, чем без них:

Вероятность же превращения удачных игрушек в неудачные после рекламы или вероятность появления неудачной игрушки после исследований будет ниже, чем без этих мероприятий:

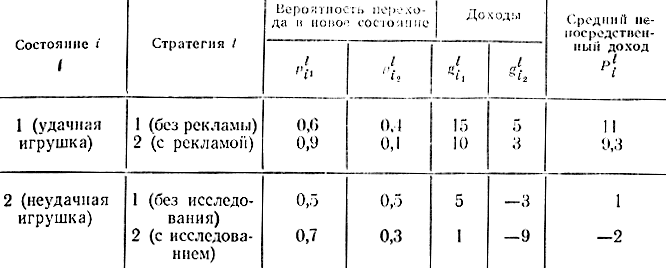
Таблица 14-9

Если же после рекламы игрушка окажется неудачной, доход все же будет больше, чем без рекламы, так как она несколько уменьшит неудачность. В случае неудачной игрушки, появившейся после исследований, доходы, естественно, будут еще меньше по сравнению с вариантом, когда неудачная игрушка появится после неудачной без исследований.

Допустим, мастер предполагает закрыть предприятие через k недель. Его интересует максимальная средняя прибыль за этот период при условии, что в данный момент он сделал какую-то игрушку, ориентируясь на статистику спроса.

Можно подсчитать средний выигрыш при оптимальной политике, если осталось k недель. При этом целесообразно использовать аппарат динамического программирования.

Принцип оптимальности здесь справедлив, в силу того что процесс простейший марковский. Напишем функциональное уравнение, для чего обозначим через S_k(i) ожидаемый доход при k-шаговом процессе, если начать из состояния i (i=1, ..., М) и использовать оптимальную политику, и через М число состояний (в нашем случае М=2). Тогда

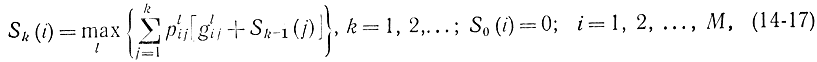
где l - номер стратегии (l= 1,2, ..., Q_i). В нашем примере Q₁=Q₂=2.

Дадим пояснение к формуле (14-17). Если до передачи производства осталось две недели (k=2) и планирование начинается с i-й игрушки, то оптимальная стратегия в соответствии с формулой (14-17) может быть подсчитана как

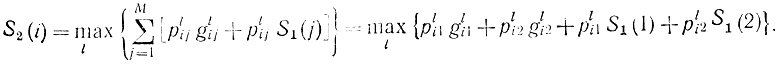
Здесь два последних члена представляют собой математическое ожидание дохода при проведении оптимальной политики на первом с конца этапе, которая может начинаться или с игрушки 1, или с игрушки 2. Вероятность первого случая равна p^l_i1, так как по условию двухэтапный процесс начинается с игрушки i-й вероятность второго случая равна p^l_i2 (рис. 14-9). Первые два члена дают математическое ожидание дохода на втором с конца этапе при стратегии l и начальной i-и игрушке; в конце этого этапа может появиться игрушка 1 с вероятностью p^l_i1 или игрушка 2 с вероятностью p^l_i2.

Рассуждая аналогично, можно убедиться в справедливости рекуррентного соотношения (14-17) для любого k. Зададим оптимальную политику вектором

определяющим выбор, который надо сделать на i-м шаге (i=1, 2, ...) при условии, что осталось k шагов. Сумма

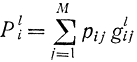
представит средний доход (математическое ожидание) для случая, когда исходным будет состояние i. Естественно, что в нашем примере из состояния i можно попасть только в одно из двух состояний с вероятностями p_i1 и p_i2. Так, для i=l=1

Средний доход P^l_i определяется только на один шаг. Поэтому он иногда называется непосредственно ожидаемым доходом. Вначале считаем, что осталось нуль недель. В этот нулевой этап S₀(i)=0. Это предположение непринципиально и сделано для простоты. Далее допускаем, что осталась одна неделя, тогда

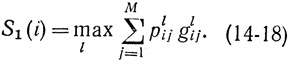
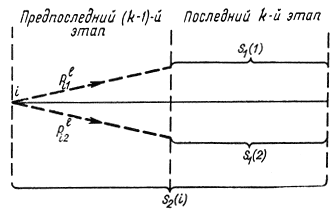
Рис. 14-9. К задаче с игрушечных дел мастер

Очевидно, что с помощью (14-17) можно вычислить эту величину для любого числа оставшихся недель. Величина P^l_i дает возможность упростить запись (14-17):

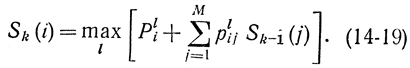
Эта формула удобнее формулы (14-17), так как вычислительной машине вектор P^l_i «запомнить» удобнее, чем матрицу ||g^l_ij||. Это выгоднее и с точки зрения объема памяти машины. Однако матрицу ||p^l_ij||. все равно необходимо запомнить для второго члена формулы (14-19).

Рассмотрим, как оптимизируется стратегия с помощью формулы (14-19) на каждом шаге, т. е. для случая, когда осталась одна, две и т. д. недели.

Для нулевого шага S₀(1)=S₀(2)=0. Для первого шага

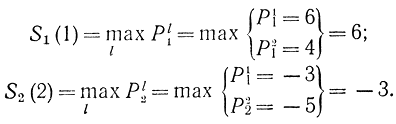
Пользуясь этими решениями и формулой (14-19), можно найти решения для второго шага и т. д. Результаты расчетов сведены в табл. 14-10.

Таблица 14-10

Благодаря рекуррентному методу динамического программирования процесс может сходиться при k→∞ к некоторому установившемуся состоянию. В данном примере - это стратегия 2. Однако часто процесс носит колебательный характер и трудно определить одну стратегию для всех k.

Рассмотренный метод с успехом может быть применен к другим условиям и вообще к решению других стохастических задач, с которыми можно познакомиться в специальной литературе [Л. 89].