14-11. Модель много шагового процесса управления

В результате развития дискретных методов оптимизации появилась новая модель процессов - много шаговый дискретный процесс. В настоящем параграфе дано обобщение рассмотренных в данной главе задач в виде общей теории много шаговых процессов.

Процедура сведения реального процесса к поэтапному, много шаговому является необходимым условием для применения дискретного Динамического программирования. Эти процессы требуют нового способа описания, отличного от методов алгебраических, дифференциальных, разностных и интегральных уравнений [Л. 90].

Рассмотрим кратко математическое описание много шаговых процессов. Будем считать, что состояние системы описывается вектором

которому в пространстве состояний соответствует некоторая точка из множества R. Для много шаговых процессов это множество состоит из дискретных точек:

каждая из которых имеет s координат. Причем можно указать преобразование

которое переводит одну точку множества R в другую точку, принадлежащую тому же множеству. Такая бесконечная последовательность называется многошаговым процессом и условно обозначается как [х, f(х)] или [х, f]. Обращаем внимание на то, что для задания много шагового процесса следует указать пару значений: начальный символ х=х⁰ и преобразование f. Обычно на практике рассматривают часть много шагового процесса - N-шаговый процесс, состоящий из последовательности векторов

При оптимизации рассматривают некоторые функции

зависящие от этого процесса и представляющие собой

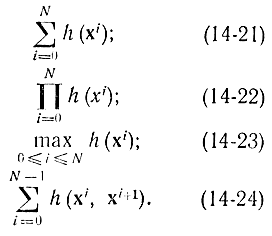
Следует обращать внимание на то, что согласно формуле (14-20) текущее k-е состояние зависит только от предыдущего (k-1)-го состояния и не зависит от более ранних, т. е. (k-2)-го, (k-3)-го и т. д. Это означает, что N состояние может быть получено из любого i-го состояния (N-i)-кратным применением преобразования

В частности, х¹=f(х), где (х=х₀) -любое начальное состояние, а также

или условно

При этих условиях для всех функций вида (14-21) - (14-24) можно вывести рекуррентное функциональное уравнение Беллмана. Так, для функции (14-21) можно написать:

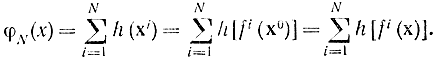
Нетрудно видеть, что для N≥1

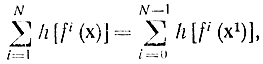
где условно принято, что х=х⁰, т. е. начальное состояние может быть любым, и f⁰(х)=х. Поэтому

Аналогично можно получить соотношения для функций (14-22)- (14-24):

Для полной формализации процесса оптимизации задач управления необходимо ввести в рассмотрение вектор управления u={u₁, u₂,...,u_l}, оптимальные значения которого требуется найти. Итак,

Тем самым обеспечивается справедливость принципа оптимальности Беллмана, состоящая в том, что каковы бы ни были первоначальное состояние (x=x⁰) и первоначальное решение (u=u⁰), последующее решение должно определять оптимальную стратегию относительно состояния, полученного в результате первоначального решения.

Так же как и в гл. 12 при выводе функционального уравнения Беллмана для непрерывного случая, в данном дискретном случае функция Беллмана зависит от начального состояния (x=x⁰) и начального управления (u=u⁰). Для удобства и учитывая, что в динамическом программировании начальное состояние считается произвольным, вместо обозначений x⁰ и u⁰ в дальнейшем используем обозначения x и u.

Далее, наряду с функцией преобразования на каждом этапе (14-25) введем функцию дохода g_i(xⁱ, uⁱ). При этом удобно представить весь много шаговый процесс в виде блок-схемы (рис. 14-10). Определим такие оптимальные значения uⁱ, при которых некоторая функция I(x⁰, x¹,...; u⁰, u¹,...) принимала бы максимальное значение. В наиболее распространенном случае

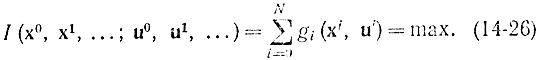
Помимо критерия (14-26) можно взять критерии

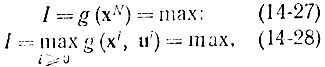
При использовании (14-27) управление становится терминальным. Часто в этом случае задачу сводят к задаче Майера введением дополнительной координаты x_s+1=g(х), которая должна обращаться в максимум: x_s+1=max. В более общем случае может потребоваться обращение в максимум выражения

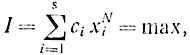
где c_i - некоторые числа, одновременно все не равные нулю. Критерий (14-28) связан с бесконечным много шаговым процессом, для которого N→∞

Для случая (14-26) введем функцию Беллмана

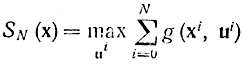
или

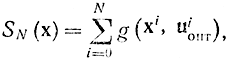
где u_опт — оптимальные стратегии. Кроме того, если учесть ранее использованные обозначения, то

Для вывода функционального уравнения за-метим, что

Это соотношение справедливо для любых начальных u⁰. Для определения оптимального дохода за N шагов необходимо взять максимум по u⁰. Поэтому

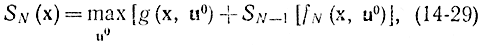
где

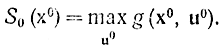
Повторяя аналогичный вывод для критерия (14-17), получаем соответственно функциональное уравнение Беллмана в виде

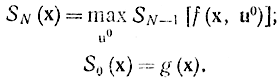
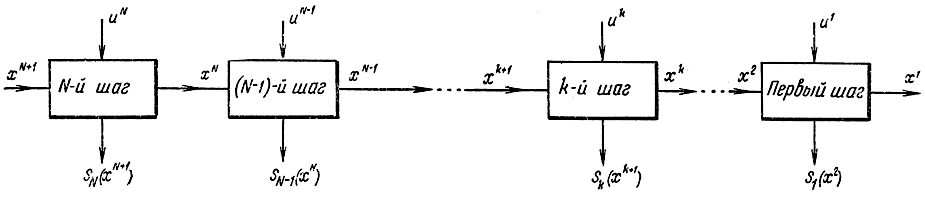
Рис. 14-10. Блок-схема много шагового процесса для динамического программирования

Для задачи распределения ресурсов уравнение (14-29) имеет вид:

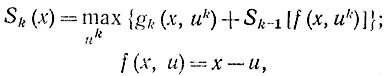
где x — общее значение исходного капитала; u — капитал, вкладываемый в очередную новую отрасль. Здесь заменили u⁰→u^k, так как последний k-й этап совпадает с выбором начального управления и поставили условие распределения одного ресурса.