14-12. Дискретный принцип максимума Понтрягина

Аналогично дискретному динамическому программированию разработан дискретный вариант принципа максимума Понтрягина [Л. 88]. Из сравнения этих двух методов видно, что вычислительные процедуры в них существенно различны. Как показано, часто в случае применения дискретного принципа максимума время вычислений значительно меньше, чем при использовании динамического программирования. Существует несколько разновидностей формального аппарата дискретного принципа максимума. Здесь будет рассмотрен простейший случай многоступенчатого процесса без обратной связи.

Представим процесс (рис. 14-11) в виде последовательности N этапов (ступеней). Здесь использована другая нумерация ступеней, нежели в аналогичной блок-схеме динамического программирования, приведенной на рис. 14-10. Считается, что

или

где

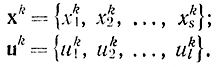
Рис. 14-11. Блок-схема много шагового процесса для дискретного принципа максимума

В отличие от аналогичного соотношения динамического программирования в формуле (14-30) координата на k-м шаге зависит от координаты на предыдущем (k—1)-м шаге и управления на k-м шаге, а не от управления на (k—1)-м шаге. Однако в большинстве случаев это отличие непринципиально и скорее зависит от того, что понимается под управлением на данном и предыдущем шагах. Кроме того, здесь считается, что функция преобразования состояний в общем случае зависит от номера шага k.

Уравнения дискретного принципа максимума. Сначала получим аналог уравнений Гамильтона - Эйлера:

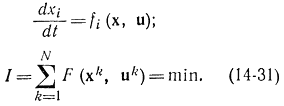
Здесь, так же как в гл. 11, весь временной интервал изменения [t₀, t₁] разбит на N отрезков длиной Δt. Если критерий оптимальности задан в виде

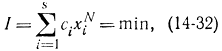
то можно положить:

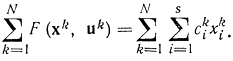
Приняв все c^k_i=0 при k≠N и c^N_i=c_i видим, что формулы (14-31) и (14-32) совпадают.

Далее введем в рассмотрение функции Лагранжа и Гамильтона:

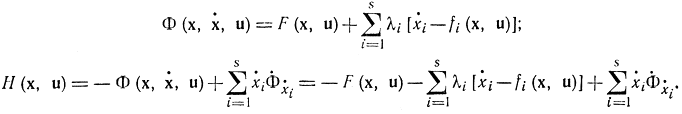
Пользуясь новыми переменными p_i=ψ_i=λ_i=Φ_xi, получаем:

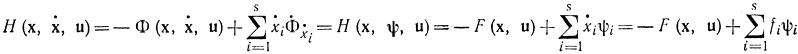
или в результате замены x_i=φ_i(x,ψ)

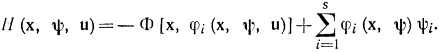
Выполняя дифференцирование по ψ_i и x_i, получаем:

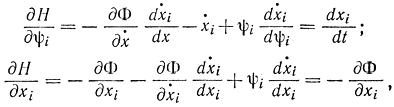
т. е. зависимость Н от F совпадает по форме с зависимостью Н от Φ. Используя дифференциально-разностное уравнение Эйлера

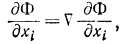
окончательно получаем дифференциально-разностные уравнения Понтрягина в виде

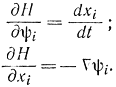
Теперь рассмотрим принцип максимума Понтрягина для случая, когда динамика системы задана разностными уравнениями вида

или

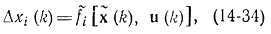
где

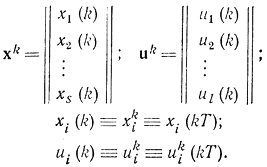
Форма (14-34) легко может быть получена из (14-33), если учесть, что

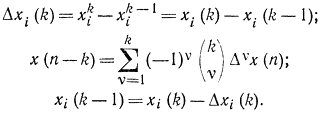
При этом

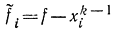
и размерность векторах x(k) в выражении (14-34) в 2 раза больше, чем размерность вектора x^k в (14-33) за счет добавления новых s разностных уравнений и компонент:

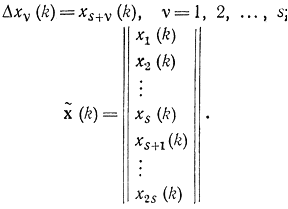
Могут встречаться и другие формы задания динамики системы в виде разностных уравнений. И, естественно, форма уравнений Понтрягина будет различная. Это лишний раз подтверждает, что дискретные процессы обладают большим многообразием, чем непрерывные. Однако все дискретные процессы, как и различные Дискретные формы задания динамики, совпадают с непрерывными при стремлении интервала дискретности к нулю.

Форма задания (14-33) удобна для вычисления в конкретных примерах, а (14-34)- при аналитических выкладках, выполняемых по аналогии с непрерывным случаем.

С помощью приемов, аналогичных ранее использованным, можно получить дифференциально-разностные уравнения Понтрягина для обоих случаев (14=33) и (14=34). Пусть задача ставится в виде

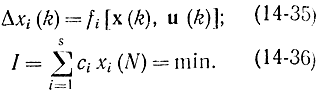
Вводя в рассмотрение функции ψ_i, удовлетворяющие системе разностных уравнений

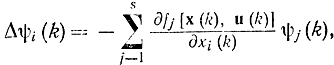
сопряженных системе уравнений для вариаций δx_i(k), полученных из (14-35),

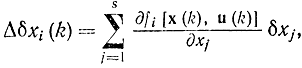
а также функцию Понтрягина

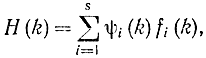
получаем уравнения принципа максимума Понтрягина в виде

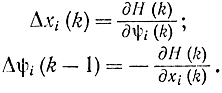
Если задача ставится в форме

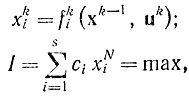
то можно получить уравнения: для вариаций δx_i

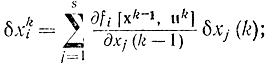
для функций ψ^k_i

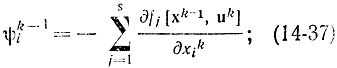
для функции Понтрягина

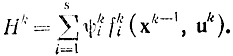
Здесь k=1,2,...,N

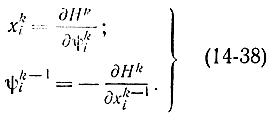
Решения этих уравнении должны удовлетворять граничным условиям

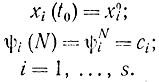
В качестве начального времени t₀ может быть взято t₀=0. Второе условие специально выбрано в соответствии с методом конструирования функций, так же как в непрерывном принципе максимума

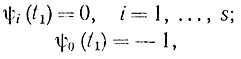
для того чтобы в конце интервала функция Понтрягина H, равная I, приняла максимальное значение:

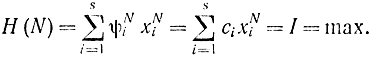
Аналогичным образом для случая, заданного формулами (14-35) и (14-36),

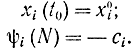
В другом варианте формализма можно, аналогично непрерывному случаю, ввести в рассмотрение еще одно уравнение и координату

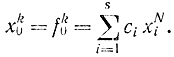
Тогда

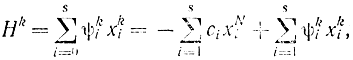
где уже использовано условие ψ^N_i=c_i. При этом H^N=max=0.

Отметим некоторые особенности приведенных выше уравнений. Хотя аргумент - время во всех функциях H, ψ, x меняется дискретно, считается, что сами функции H, ψ, x могут изменяться непрерывно и Дифференцируемы. Функция H зависит от номера k (ступени, шага), что эквивалентно зависимости от времени или зависимости функции Беллмана S_k от номера шага. В задачах, решаемых с помощью дискретного принципа максимума, так же как в задачах, решаемых с помощью дискретного динамического программирования, в исходной постановке время может отсутствовать. В таком случае его вводят искусственно, создавая эквивалентную модель много шагового процесса. Тогда функция Понтрягина Н(k) или Н^k принимает максимальное значение при оптимальном управлении, т. е.

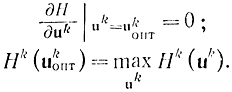
Дифференциально-разностные уравнения Понтрягина являются необходимыми условиями экстремума функции. Для линейных разностных уравнений эти условия являются (так же, как и в непрерывном случае) достаточными. Для выпуклых функций и, в частности, для линейных функций они определяют глобальный экстремум.

Кроме того, дискретные процессы, как уже указывалось ранее, обладают большим разнообразием, чем непрерывные. В частности, как будет показано на примере ниже, при одних k функция H^k принимает максимальное значение, а при других k - минимальное. Поэтому говорят, что дифференциально-разностные уравнения Понтрягина определяют не оптимальные, а стационарные решения или точки фазового пространства. В частности, можно показать, что оптимальное управление существует для любого начального состояния x⁰ и удовлетворяет условию

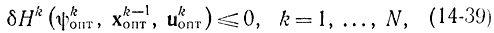
где оптимальные значения сопряженных переменных ψ^k_опт определяются из сопряженной системы уравнений (14-39) с граничными условиями

Кроме того, можно показать, что если для какого-нибудь k точка u^k_опт является внутренней точкой множества U допустимых значений управления, то δH^K(u^k_опт)=0, а если в точке u^k_опт отсутствует такая допустимая (не выводящая из области U) вариация δu^k, при которой δH^k(u^k_опт)<0, то эта точка является граничной точкой множества U [Л. 88]. Поэтому, если нет ограничений на управляющие воздействия, при оптимальном управлении δH^k=0.

Условие δH^k<0, т. е. условие локального или глобального максимума, может выполняться только на границе области U.

Пример 14-3. Динамика дискретной системы определяется уравнениями [Л. 88]

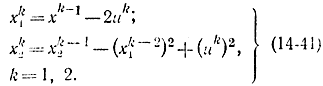
Диапазон измерений управляющих воздействий ограничивается соотношением

начальные условия задаются в виде

Требуется найти оптимальное управление u₁ и u₂, обращающее функцию I=x²₂ в максимум при ограничениях (14-42). Выразим из уравнений (14-41) x²₂=f²₂(u₁, u₂) и определим значения u_1опт и u_2опт) доставляющие максимум этому выражению. В результате получим:

Функцию Понтрягина для этого случая запишем в виде

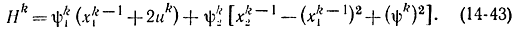
Оптимальные значения x^k_опт и ψ^k_опт найдем из соотношений (14-41):

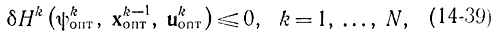
В результате получим:

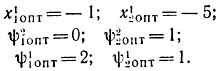
После подстановки этих значений в формулу (14-45) получим:

Нетрудно убедиться, что H² достигает максимального значения при u_2опт=±5, а H¹ минимального u_1опт=-2.

Таким образом, в общем случае функция Понтрягина Н^л принимает при оптимальном управлении любое стационарное значение, необязательно являющееся максимумом, и принцип максимума Понтрягина несправедлив.

Но можно сузить класс дискретных задач таким образом, что принцип максимума Понтрягина будет выполняться. Если много шаговый процесс обладает таким свойством, при котором множество R₁(x) всех состояний х, в которые можно перевести точку х за один шаг при допустимом управлении u∈U, т. е.

является выпуклым (см. гл. 16), то для оптимальности управления необходимо, чтобы функция Понтрягина на оптимальном управлении принимала максимальное значение.

Следует заметить, что выпуклость множества R₁(x) не гарантирует выпуклости функции Понтрягина. Если функция Понтрягина выпукла, то доказанное ранее соотношение (14-39) обеспечивает справедливость принципа максимума Понтрягина.

Наконец, если функции f^k_i линейны, т. е.

где k=1,..., N; А^k-1 - матрица, (s*s); В^k - матрица (s*l), функция цели

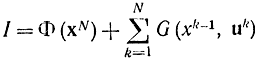
выпукла и множество допустимых значений управления U тоже выпукло, то, для того чтобы управление их было оптимальным, необходимо и достаточно, чтобы функция Понтрягина на этом управлении достигала максимального значения [Л. 88].